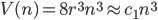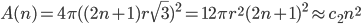Il limite alla quantità di informazione

Nel 1965 Gordon Moore (fondatore di Intel) osservando l'andamento nel periodo 1959-1965 rilevò che ogni anno la capacità di calcolo dei processori era raddoppiata. Da questo, con qualche aggiustamento, elaborò quella che oggi è nota come la Prima Legge di Moore. Come detto, più che di una legge, si tratta di un'osservazione empirica:

"La capacità di calcolo dei processori immessi sul mercato raddoppia ogni 18 mesi."

Storicamente anche dopo il 1965 la legge ha continuato a essere valida nel corso dei decenni successivi; chiamarla legge sembra un tantino ottimistico (un po' come la "Legge di Titius-Bode").

Questa legge, o questa osservazione, non può non fare sorgere, in chi ne viene a conoscenza, l'idea che la progressione a cui fa riferimento non possa, alla lunga, che terminare. Ci sarà pure un limite alla velocità di calcolo che i processori non riusciranno a raggiungere e a superare? Con questo articolo vorrei parlare non tanto di che cosa ci possiamo attendere nei prossimi anni o nei prossimi decenni nel campo della potenza di calcolo dei computer, ma di un limite teorico superiore alla capacità di calcolo, che costringerà, presto o tardi, la nostra curva, a piegare verso un asintoto orizzontale.

 

Il limite di Bekenstein

Diamo innanzitutto un limite estremo a questa espansione. In particolare, qual è la massima quantità di informazione che può essere confinata in una unità di volume? Certo si tratta di un limite molto drastico che nulla ci dice rispetto alla lunga strada che servirà per avvicinarci; ma almeno si tratta di un limite in qualche modo certo e ineliminabile.

Ci viene in aiuto, in questo caso, la Termodinamica dei buchi neri. In particolare esiste un teorema, di Bekenstein-Hawking, che definisce proprio la quantità di informazione che può essere contenuta in una unità di volume nell'universo. Sorprendentemente questa quantità è limitata dalla superficie e non dal volume stesso il che, se ci si pensa, è piuttosto strano (ammesso che possa esserci qualcosa di non particolarmente strano parlando di Termodinamica dei buchi neri...).

Il teorema afferma infatti che l'entropia è data da:

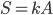
dove:

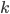• è una costante (che il teorema precisa essere in relazione con la lunghezza di Planck e la costante di Boltzmann; per i nostri ragionamenti ci basta considerare che si tratti di una costante di proporzionalità);
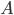• è l'area del volume di universo considerato.

 

Qual è quindi la relazione che intercorre fra la capacità di calcolo di un processore e una quantità persino difficile da descrivere come l'entropia?

Cominciamo con il dire che l'entropia, in termodinamica, misura il disordine di un sistema fisico. Il disordine è un concetto non particolarmente chiaro ed evidente, che risulta più comprensibile (anche senza diventare mai particolarmente digeribile), fornendo degli esempi di stati ordinati. Ad esempio: una scatola di cartone che contiene sedici cubetti di cui 8 rossi e 8 bianchi possiamo considerare che sia in uno stato ordinato quando gli 8 cubetti rossi si trovano tutti "da una parte" e i rimanenti 8 cubetti bianchi tutti dall'altra. Avremo invece uno stato tanto più disordinato quanto più i cubetti di vari colori sono mischiati fra loro. (Nota: questa assunzione non ha un vero senso fisico: è solo una convenzione dal momento che, da un punto di vista puramente concettuale, ogni disposizione dei 16 cubetti può essere identificata come quella "ordinata" e il "disordine" semplicemente come la distanza dalla configurazione "scelta". Ma semplifichiamoci per un attimo la vita e associamo l'ordine alla configurazione se non più ordinata, quantomeno più facile da visualizzare).

Dato che l'entropia misura il disordine, potremo dire che la situazione in cui i cubetti sono mischiati è associata a un'entropia maggiore rispetto a quella in cui i cubetti sono nettamente separati. Questo porta al poter formulare il secondo principio della termodinamica in termini (non rigorosi) di entropia:

L'entropia di un sistema chiuso aumenta con il tempo.

Che è equivalente a dire: in un sistema chiuso, con un corpo più caldo e uno più freddo, il calore tende a fluire naturalmente dal caldo al freddo fino a far raggiungere ad entrambi l'equilibrio.

Tornando quindi alla nostra scatola di cubetti: che cosa succede se qualcuno scuote la scatola? Possiamo fare una predizione supportata dal secondo principio: l'entropia (cioè il disordine) aumenterà. Quantomeno: statisticamente aumenterà. Certo è anche possibile che da una situazione disordinata, dopo aver scosso la scatola, la riapriamo e troviamo tutti i rossi a destra e tutti i bianchi a sinistra; ma statisticamente è estremamente improbabile.

In effetti se consideriamo quante possibilità abbiamo di trovare i cubetti ordinati, possiamo dire che, considerando le 8 posizioni a destra (o a sinistra indifferentemente), quante possibilità ci sono che siano occupate solo da cubetti bianchi?

• Per la prima posizione abbiamo 8 possibilità (pari al totale dei cubetti bianchi) su 16 (totale dei cubetti da cui possiamo estrarre);
• Per la seconda posizione abbiamo 7 possibilità (pari al totale dei cubetti bianchi rimanenti) su 15 (totale dei cubetti rimanenti da cui possiamo estrarre);

e così. Il calcolo in generale porta a dire che la probabilità è data da:

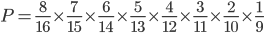
Ma questo numero è circa 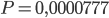(o, equivalentemente 0,0077%). Parliamo quindi di una possibilità remota ma non del tutto esclusa in via teorica.

Qual è l'attinenza dell'entropia termodinamica con la quantità di informazione? Con un improvviso salto in avanti, possiamo affermare che sono due grandezze che misurano la stessa cosa. Chi necessita di maggiori informazioni (ops!) a riguardo, può consultare molte fonti in rete a cominciare da questa. Dopo questo approfondimento o facendo un "pigro" atto di fede, passiamo oltre.

 

Una porta lasciata insospettabilmente aperta

Torniamo ora al teorema di Bekenstein-Hawking. Perché abbiamo definito come sorpredente il fatto che la quantità di informazione è limitata dalla superficie e non dal volume? La ragione è data da un semplice studio di funzione. Immaginiamo di avere, in un dato punto dello spazio, un elemento in grado di contenere informazioni; per visualizzare il concetto, possiamo immaginarcelo come una unità di memoria di un calcolatore. Questo nostro elemento conterrà una quantità 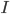di informazioni e, qualunque sia la sua forma, possiamo immaginare che sia contenuto entro un raggio 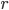. Se noi accostiamo a questo elemento ad altri suoi elementi simili in tutte le direzioni dello spazio, possiamo supporre di mettere un elemento simile sopra e uno sotto, uno a destra e uno a sinistra, uno davanti e uno dietro. Il "cubo così ottenuto possiamo immaginare di riempirlo con gli ulteriori 8 cubetti che toccano il cubetto iniziale solo agli spigoli.

Che cosa otteniamo?

• Nello stato iniziale abbiamo un cubo che possiamo circoscrivere in una sfera di raggio 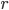; questo volume conterrà una quantità 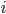di informazione e sarà delimitato da una superficie (quella della sfera), data da .
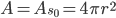• Dopo aver aggiunto gli ulteriori cubetti, otteniamo di avere un cubo maggiore, di lato 3 cubetti. Il volume del cubo sarà dato al numero dei cubetti, quindi 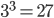quindi 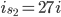mentre la quantità di informazione sarà proporzionale alla superficie della sfera che contiene il cubo maggiore (quantomeno: limitata dalla superficie stessa). Ma anche il calcolo della superficie è semplice: se consideriamo la diagonale del cubo, otteniamo che essa misura 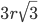(ricordando che il lato di ogni cubetto è 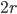), da cui la sua superficie è .
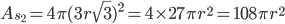• Ripetiamo l'operazione, aggiungendo ulteriori cubetti di "memoria" fino a ottenere un ulteriore cubo si lato 5. Per gli stessi ragionamenti si ottiene che 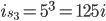. Ma quale sarà il raggio della sfera che può circoscrivere il nostro cubo? Anche qui è facile trovare la regola generale... In effetti la semidiagonale del cubo composto dall'accostamento di cubetti da un lato e subetto dall'altro (intendendo: in ogni direzione dello spazio) è data da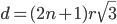

Le formule generali che forniscono Volume e Superficie sono quindi:

 

Ma questo ha delle conseguente piuttosto importanti: la prima curva è una cubica e rappresenta la quantità di materia che possiamo immaginare di confinare nella nostra ipotetica accumulazione di unità di memoria (qualcosa di simile alla Biblioteca di J.L. Borges).

La seconda curva è una parabola e rappresenta la quantità massima di informazione che può essere racchiusa all'interno del volume di spazio che stiamo considerando.

Quindi, se consideriamo il primo cubetto, avremo che questo contiene una certa quantità di informazione e che questa cresce come 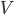mentre la quantità massima di riferimento cresce come .

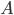Un semplice studio di funzione ci mostra che esiste un certo numero , cioè una certa dimensione del cubo (grande come un campo da calcio? Grande come una stella supergigante? Grande come un ammasso di galassie?: non importa) per il quale la cubica supererà la parabola. E questo ci è mostrato semplicemente dal limite seguente:

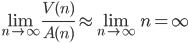
La conseguenza di questa affermazione è che per un sufficientemente grande è possibile immaginare un accumulo di informazioni maggiore del massimo teoricamente previsto. Oppure, detto in termini più evocativi: L'Universo potrebbe riuscire a contenere le informazioni necessarie a comprendere interamente se stesso. Il che, se ci pensate, è un paradosso di ricorsività...

 

Est ordo in rebus

Fortunatamente le cose non sono poi così brutte come potrebbero apparire; anche in questo caso, come già nel caso del diavoletto di Maxwell, l'intima coerenza dell'Universo ci rivolge il suo occhio benevolo e non ci obbliga, nemmeno questa volta, ad arrenderci all'irrazionalità. L'esempio a cui mi riferisco è un esperimento mentale che si basa sugli elementi seguenti:

• La temperatura di un corpo (per semplicità: di un gas) è un indice dell'agitazione media delle sue molecole;
• che cosa succederebbe se un diavoletto (cioè un essere che in astratto abbia la possibilità di interagire con la materia in modi che non ci interessa qui approfondire) spostasse tutte le molecole con un moto più "rapido" (quindi: più calde) e le mettesse da una parte e spostasse allo stesso tempo tutte le molecole più fredde dall'altra? Questo diavoletto non avrebbe di fatto contraddetto il secondo principio della termodinamica, cioè quello che prescrive l'irreversibilità dei fenomeni fisici?
• Se mai questo diavoletto (o un qualsiasi suo surrogato termomeccanico) esistesse, due corpi, uno caldo e uno freddo, che posto a contatto abbastanza a lungo abbiano portato le loro temperature all'equilibrio, potrebbero di nuovo diventare uno caldo e uno freddo?

 

In questo caso chi interveniva a toglierci le castagne dal fuoco? Interveniva la stima che il diavoletto dovrebbe compiere un lavoro (in senso fisico) pari all'energia ottenuta con la separazione delle molecole calde da quelle fredde. E questo fatto conciliava l'apparente contraddizione, pur se in tutta la sua ipoteticità, con un elegantissimo: "Se mai esistesse, comunque non violerebbe la seconda legge perché qualsiasi diavoletto compirebbe un lavoro sulle molecole che compenserebbe l'aver riportato indietro gli stati".

E' chiaro che quanto ho scritto sopra non ha nessun rigore; ci sono molte fonti in rete che possono fornire i dettagli puntuali di quanto affermo. A me serviva solo suggerirne l'idea.

In effetti, la valutazione delle due curve del volume e della quantità di informazione sembra proprio un diavoletto di Maxwell dell'entropia che porti a contraddire il teorema di Bekenstein-Hawking... Eppure, anche in questo caso, esiste una considerazione che ci toglie brillantemente da ogni impiccio.

Di fatto ogni massa che noi poniamo nello spazio è soggetta all'attrazione gravitazionale. All'aumentare della massa che affastelliamo (nel nostro esperimento mentale) vicina alla massa precedente, la forza di gravità esercitata dalle masse, aumenta. Questo aumento di massa crea un effetto gravitazionale sempre più elevato.

Dove sta la soluzione al nostro paradosso? Sta nel fatto che accumulando una quantità di materia (dotata di massa) sufficientemente grande, quello che si ottiene è un pianeta, e poi una stella, e poi un... buco nero. Cioè: una singolarità dell'universo in cui non valgono né le leggi fisiche ordinarie né si sa di preciso che cosa valga...

Questo per significare che, anche se vale il teorema di Bekenstein-Hawking, in realtà non è possibile immaginare un calcolatore che riesca a contenere più informazioni di quelle che descrivano interamente il volume di universo in esso contenuto. Arrivati a una determinata quantità di massa, il "calcolatore" si trasforma irreparabilmente in un buco nero. Ed ecco trovato l'asintoto.