Ho un ricordo molto distinto, anche a distanza di anni (ahimè!) di un preciso giorno del Liceo. È il ricordo di quando il professore di Scienze Naturali, con la barba foltissima e il camice bianco, che scendeva fino sotto le ginocchia, ci parlò della Legge di Titius-Bode. Lo fece, nella sua cadenza bergamasca ormai annacquata da anni di periferia milanese, con lo sguardo vago, come ad introdurci in punta di piedi verso uno dei misteri del cosmo.
"La legge di Titius-Bode è una di quelle leggi strane, misteriose, che non è ben chiaro per quale ragione funzionino ma che, effettivamente, funzionano."
Con questo articolo vorrei esprimere le ragioni che ci possono portare, con grande serenità, a rifiutare questa legge. E a sostenere che: non funziona affatto!
Descrizione della legge e ragioni del suo successo
La legge di Titius-Bode è una regola matematica che cerca di descrivere (e prevedere) la distribuzione dei pianeti all'interno del sistema solare. In particolare descrive le loro progressive distanze dal sole in funzione della seguente regola numerica empirica:
Sia 
il semiasse maggiore dell'orbita di un pianeta, allora la legge di distribuzione è data da:
per 
che assume i valori 0, 3, 6, 12, 24, 48, ecc.
Per rendere il tutto più facilmente computabile, è stata con il tempo introdotta una formulazione, del tutto equivalente, in questo modo:
per 
dove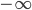 
è un valore di comodo per far azzerare il secondo termine, ponendo che 
.
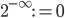Indipendentemente dalla formulazione operativa, la tabella dei valori calcolati è la seguente:
| i | Valore secondo Titius-Bode |
|---|---|
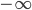| 0,4 |
| 0 | 0,7 |
| 1 | 1 |
| 2 | 1,6 |
| 3 | 2,8 |
| 4 | 5,2 |
| 5 | 10 |
| 6 | 19,6 |
Ma questa tabella si relaziona molto bene con le distanze progressive dei pianeti dal Sole, come mostra l'ulteriore tabella:
| i | Valore secondo Titius-Bode | Distanza del pianeta |
|---|---|---|
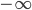| 0,4 | 0,3871 UA (Mercurio) |
| 0 | 0,7 | 0,7233 UA (Venere) |
| 1 | 1 | 1 UA (Terra) |
| 2 | 1,6 | 1,5237 UA (Marte) |
| 3 | 2,8 | ??? |
| 4 | 5,2 | 5,2034 UA (Giove) |
| 5 | 10 | 9,5371 UA (Saturno) |
| 6 | 19,6 | 19,1917 UA (Urano) |
Certo: c'è un posto vuoto, fra Marte e Giove, ma persino Urano trova ottimamente posto in questa successione. Nella tabella le distanze sono espresse in UA, cioè Unità Astronomiche, un'unità di misura posta per convenzione uguale alla distanza media Terra-Sole, cioè circa 150 milioni di chilometri.
Occorre innanzitutto notare che quanto espresso dai due sapienti settecenteschi è semplicemente il meccanismo universale attraverso il quale procede la scienza: si osservano i dati sperimentali, si formula un'ipotesi, si predicono delle conseguenze per via logica (in questo caso: matematica), si stabiliscono dei test che possono rafforzare l'ipotesi o smentirla, e via discorrendo.
Che cosa è successo, quindi, dopo la formulazione di questa legge, che abbia portato a conservarla? E' successo, banalmente, che la legge ha funzionato, più o meno bene, in funzione di questi eventi succesivi:
- La legge fu pubblicata nel 1772 quando, rispetto all'ultima tabella sopra riportata, c'era il posto vuolo per
e l'ultimo numero era 
corrispondente all'ultimo pianeta allora conosciuto, cioè Saturno; - Il 13 marzo 1781 William Herschel scoprì il pianeta Urano (o, meglio: si rese conto che la piccola stellina classificata come tale da decine di anni, in realtà si spostava: era un pianeta!). Urano si collocava proprio alla distanza predetta da
. - Il 1° gennaio 1801 l'astronomo Giuseppe Piazzi scoprì Cerere "esattamente" dove previsto dalla legge di Titius-Bode per
In questo modo la tabella veniva meravigliosamente a completarsi. Quali ragioni potrebbero mai sorgere per confutarla, dato che è stata addirittura in grado di formulare ipotesi (per e ) poi verificate sperimentalmente come è proprio della migliore scienza?
Ragioni astronomiche per rifiutarla
Eppure le ragioni per rifiutarla, fin dal suo apparire, non mancano. La prima, la più banale, riguarda il fatto che si riesce ad applicarla esclusivamente ai pianeti del sistema solare. Ad esempio: non si riesce ad applicare nemmeno ai satelliti di Giove, di Saturno o di altri pianeti (il sistema Terra-Luna non fa testo dato che non ci sono altri satelliti naturali da mettere in successione di distanza).
Negli ultimi anni, inoltre, con la scoperta ormai di migliaia pianeti extrasolari, la struttura del nostro sistema planetario appare sempre più come un'eccezione. Vedi ad esempio: "Chaotic Disintegration of the Inner Solar System - K. Batygin, A. Morbidelli, M. J. Holman" per una visione di come il nostro sistema solare si è evoluto in maniera caotica. Di fatto pare che la struttura di pianeti (piccoli e rocciosi vicini al sole, giganti gassosi più lontani) sia assolutamente un'eccezione. Una legge matematica che descriva questa eccezione, va da sé che non ha molte speranze di essere una legge universale del cosmo.
E il fatto che non valga nel piccolo (satelliti del nostro sistema solare) né nel grande (altri sistemi planetari) porta a ritenerla, astronomicamente parlando, più un caso che un meccanismo capace di descrivere un meccanismo più profondo, su cui valga la pena indagare.
Ragioni matematico-analitiche per rifiutarla
Tuttavia, si potrebbe essere portati a pensare che, anche fosse solo ai pianeti del sistema solare, la descrizione della loro progressione sia abbastanza fedele. In realtà nemmeno questo è poi così vero... Consideriamo, ad esempio, il problema delle distanze dai pianeti al contrario, cioè partendo dalle distanze note e cercando di determinare quale relazione le leghi.
Di fatto i pianeti, a oggi, sono certamente 8: Mercurio, Venere, Terra, Marte, Giove, Saturno, Urano e Nettuno. Cerere e Plutone, per ragioni astronomiche e non solo di definizione, hanno perso da tempo questa caratterizzazione e non sono considerati pianeti più di quanto lo siano le comete. La domanda che ci potremmo porre è:
"non possono esistere altre funzioni "generatrici" che approssimano meglio la sequenza dei numeri che ci proponiamo di determinare?"
La risposta è: certamente. Anzi: infinite. Vediamo il caso più banale di determinare una polinomiale approssimante, cioè di una funzione esprimibile semplicemente come:
La nostra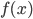 
deve essere tale che valgano le seguenti ipotesi:
, 
, 
...e così via per gli altri 5 valori riferiti a pianeti (Qui considero anche Cerere solo per completezza). Queste ipotesi portano molto semplicemente a dire che occorre trovare la soluzione del seguente sistema di equazioni lineari di primo grado:
Ma questo è un sistema di 8 equazioni in 8 incognite che quindi ammette soluzione (dato che il suo determinante è non nullo). In particolare si ottiene come soluzione il valore dei vari 
che porta la funzione a poter essere scritta come:
Quindi esiste almeno una legge che approssima meglio il reale comportamento della distribuzione dei pianeti. Almeno questo ci può portare a considerare che la Legge di Titius-Bode se già non ha altri ambiti di applicazione oltre ai pianeti del sistema solare, nemmeno per il sistema solare è la legge migliore che si possa determinare...
Ragioni statistiche per rifiutarla
Ultima domanda che ci possiamo porre: ma la legge di Titius-Bode predice davvero con accuratezza le distanze dei pianeti dal Sole? La prima risposta è banalmente un'altra domanda: Cerere è un pianeta?
Perché se la risposta alla domanda è sì, allora la legge non è utilizzabile perché non descrive tutti gli altri corpi "pianeti tanto quanto Cerere", vale a dire: Pallade, Vesta, Plutone, Sedna, ecc.
Se la risposta è no, allora rimane un buco insanabile nella formulazione (per ).
Per tutte queste ragioni è più prudente considerare la legge un buon tentativo; una cosa che sembrava vera ma che, alla prova dei fatti, non ha retto. Onore al merito di chi ci ha provato.