Immaginiamo il piano Euclideo  , cioè l'insieme di tutti i punti esprimibili come coppia di coordinate
, cioè l'insieme di tutti i punti esprimibili come coppia di coordinate 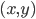 con
con 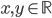 . Immaginiamo di partire da un determinato punto, mettiamo per semplicità, di partire dal punto in cui si pone solitamente l'intersezione degli assi cartesiani, cioè il punto
. Immaginiamo di partire da un determinato punto, mettiamo per semplicità, di partire dal punto in cui si pone solitamente l'intersezione degli assi cartesiani, cioè il punto 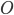 di coordinate
di coordinate 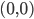 , chiamato origine.
, chiamato origine.
Immaginiamo ora di spostarci da questo punto (cioè di raggiungere punti aventi altre coordinate) limitando però la nostra possibilità di spostamento. Non ammettiamo tutti gli spostamenti possibili; ammettiamo esclusivamente quelli effettuati tramite riga e compasso. In questo modo raggiungeremo tutti i punti del piano  o solo un loro sottoinsieme? Scopo di questo articolo è mostrare come la risposta a questo quesito e a quello dell'articolo sulla duplicazione del cubo, pur non coincidendo, siano intimamente correlate.
o solo un loro sottoinsieme? Scopo di questo articolo è mostrare come la risposta a questo quesito e a quello dell'articolo sulla duplicazione del cubo, pur non coincidendo, siano intimamente correlate.
Il secondo punto
In effetti partire dalla sola origine 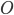 è un po' poco. Fino a quando non abbiamo almeno un altro punto qualsiasi, non possiamo, a voler essere rigorosi, nemmeno parlare di assi cartesiani (o viceversa). Questo perché un asse che contenga il punto
è un po' poco. Fino a quando non abbiamo almeno un altro punto qualsiasi, non possiamo, a voler essere rigorosi, nemmeno parlare di assi cartesiani (o viceversa). Questo perché un asse che contenga il punto 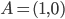 e tutti suoi "multipli" (secondo un senso che sarà ulteriormente da precisare), equivale ad avere un secondo punto base. E viceversa nulla impedisce, dato un punto generico
e tutti suoi "multipli" (secondo un senso che sarà ulteriormente da precisare), equivale ad avere un secondo punto base. E viceversa nulla impedisce, dato un punto generico 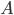 di considerare proprio gli assi cartesiani che abbiano OA come segmento (di misura unitaria) sull'asse.
di considerare proprio gli assi cartesiani che abbiano OA come segmento (di misura unitaria) sull'asse.
Consideriamo quindi di avere 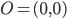 e
e 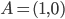 come coppia base di punti. Con le sole costruzioni tramite riga e compasso, quali altri punti di
come coppia base di punti. Con le sole costruzioni tramite riga e compasso, quali altri punti di  potremo raggiungere?
potremo raggiungere?
Facciamo alcune osservazioni preliminari.
Osservazione 1
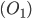 Dati
Dati 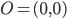 e
e 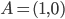 , è possibile, con riga e compasso, raggiungere il punto
, è possibile, con riga e compasso, raggiungere il punto 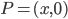 per qualsiasi
per qualsiasi 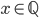 .
.
Ricordiamo che 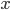 è un numero razionale, cioè
è un numero razionale, cioè 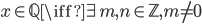 con
con 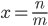
Per esibire la dimostrazione basta una semplice costruzione. Innanzitutto per costruire, dato il segmento 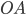 che, ricordiamo, ha misura unitaria, un segmento
che, ricordiamo, ha misura unitaria, un segmento 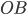 di lunghezza
di lunghezza  basta prolungare il segmento stesso, dalla parte di
basta prolungare il segmento stesso, dalla parte di 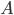 e puntare il compasso in
e puntare il compasso in 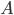 con apertura
con apertura 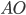 . Il punto
. Il punto 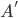 ottenuto, dalla parte opposta ad
ottenuto, dalla parte opposta ad 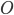 sarà ovviamente il punto
sarà ovviamente il punto 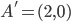 ; ripetendo per
; ripetendo per  volte l'operazione, troviamo il punto
volte l'operazione, troviamo il punto 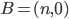 .
.
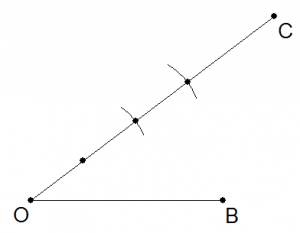
Ora occorre prendere la parte m-esima di questo segmento. Ma ancora una volta questo è possibile con riga e compasso. In particolare è sufficiente, considerando il segmento 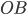 , tracciare un segmento che esce da
, tracciare un segmento che esce da 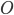 con un angolo qualsiasi. Su questo segmento iteriamo la costruzione di
con un angolo qualsiasi. Su questo segmento iteriamo la costruzione di 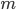 segmenti di misura uguale (medesima operazione di riportare la lunghezza
segmenti di misura uguale (medesima operazione di riportare la lunghezza 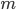 volte). Otteniamo la figura seguente:
volte). Otteniamo la figura seguente:
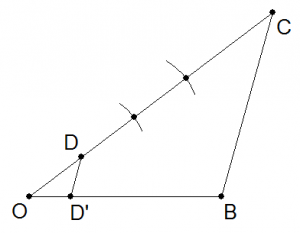
Tracciamo ora il segmento 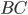 e la parallela, passante per il primo punto ottenuto sul segmento
e la parallela, passante per il primo punto ottenuto sul segmento 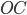 , che chiameremo
, che chiameremo 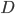 , al segmento
, al segmento 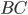 .
.
Questo segmento intercetta, sul segmento 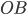 un punto
un punto 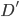 . Ma per tutto quello che abbiamo fin qui costruito, ricordando il teorema in base al quale due rette (
. Ma per tutto quello che abbiamo fin qui costruito, ricordando il teorema in base al quale due rette (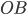 e
e 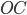 ) staccano su un fascio di rette parallele segmenti proporzionali, questo segmento avrà proprio coordinate
) staccano su un fascio di rette parallele segmenti proporzionali, questo segmento avrà proprio coordinate 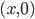 dove
dove 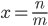 .
.
Osservazione 2
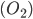 Non tutti i punti del piano sono raggiungibili con riga e compasso. Ad esempio i punti con almeno una coordinata non algebrica (cioè trascendente), non sono raggiungibili, per la definizione stessa di numero trascendente. In particolare non saranno raggiungibili i punti
Non tutti i punti del piano sono raggiungibili con riga e compasso. Ad esempio i punti con almeno una coordinata non algebrica (cioè trascendente), non sono raggiungibili, per la definizione stessa di numero trascendente. In particolare non saranno raggiungibili i punti 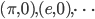 e così via per ogni coppia di numeri per cui almeno uno degli elementi sia esso stesso un numero trascendente; si tratta di punti che non possono essere costruiti, con il solo uso di riga e compasso, a partire dai nostri punti base
e così via per ogni coppia di numeri per cui almeno uno degli elementi sia esso stesso un numero trascendente; si tratta di punti che non possono essere costruiti, con il solo uso di riga e compasso, a partire dai nostri punti base 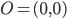 e
e 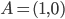 .
.
Perché non sembri che questi punti irraggiungibili siano pochi, dato il modo piuttosto "artificiale" con cui sembra che sia necessario definirli, occorre anzitutto dire che non solo questi numeri sono infiniti. Ma sono anche di un infinito non numerabile; addirittura sono proprio questi punti (=numeri) che rendono 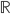 di un infinito di ordine superiore a quello di
di un infinito di ordine superiore a quello di 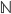 .
.
Osservazione 3
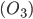 Dati
Dati 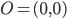 e
e 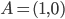 , è possibile, con riga e compasso, raggiungere anche punti
, è possibile, con riga e compasso, raggiungere anche punti 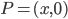 con
con 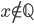 . Ad esempio è facile costruire il punto
. Ad esempio è facile costruire il punto 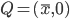 con
con 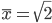 .
.
La costruzione è banale. Basta considerare i punti 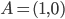 e
e 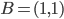 . Per il teorema di Pitagora, la misura di
. Per il teorema di Pitagora, la misura di 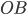 è proprio
è proprio 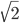 . Puntando in
. Puntando in 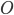 con apertura di compasso
con apertura di compasso 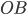 , la circonferenza che si traccia intercetta l'asse su cui si trovano
, la circonferenza che si traccia intercetta l'asse su cui si trovano 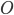 e
e 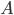 in un punto
in un punto 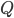 che ha proprio coordinate
che ha proprio coordinate 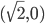 .
.
Ma allora, dove possiamo arrivare?
Abbiamo visto che possiamo arrivare da molte parti, ma non ovunque. E che questi punti raggiungibili non si limitano ai punti di coordinate razionali. Ci rimane quindi da precisare dove esattamente possiamo arrivare, cioè ci rimane di caratterizzare i nostri punti raggiungibili in termini meno vaghi.
Per ottenere questa caratterizzazione dobbiamo ripartire dal definire esattamente che cosa intendiamo, in termini rigorosi, con "costruzione con riga e compasso". Le operazioni che dobbiamo ammettere si riducono a due sole:
- Dati due punti
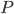 e
e 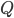 , tracciare con una riga una retta che li colleghi.
, tracciare con una riga una retta che li colleghi. - Dato un punto
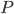 e un'apertura di compasso definita in base a due punti dati, tracciare una circonferenza con centro in
e un'apertura di compasso definita in base a due punti dati, tracciare una circonferenza con centro in 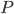 e raggio pari alla distanza dei punti.
e raggio pari alla distanza dei punti.
Osservazione 4
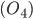 I punti raggiungibili contenuti in una retta data, sono densi nella retta ma non sono tutti i punti della retta stessa.
I punti raggiungibili contenuti in una retta data, sono densi nella retta ma non sono tutti i punti della retta stessa.
In particolare il fatto che non tutti i punti della retta siano raggiungibili deriva dall'osservazione 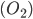 . Il fatto che i punti raggiungibili siano densi (cioè, per definizione, dati due punti
. Il fatto che i punti raggiungibili siano densi (cioè, per definizione, dati due punti 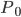 e
e 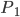
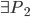 compreso fra i due
compreso fra i due 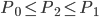 e
e 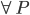
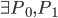 con
con 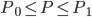 ) deriva semplicemente dalla costruzione del punto medio di un segmento, ottenibile con riga e compasso.
) deriva semplicemente dalla costruzione del punto medio di un segmento, ottenibile con riga e compasso.
Specificando meglio l'Osservazione, possiamo affermare che non sono di per sé raggiungibili tutti i punti appartenenti a un dato segmento, ma solo quelli che si trovano in una di queste condizioni:
- Sono raggiungibili tramite compasso puntato in un punto "noto" e con apertura pari alla distanza fra due punti "noti";
- Sono raggiungibili in quanto all'intersezione fra rette e/o circonferenze ottenute a partire da punti "noti".
Osservazione 5
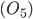 I punti raggiungibili a partire da due punti dati che, senza ledere le generalità, possiamo considerare come
I punti raggiungibili a partire da due punti dati che, senza ledere le generalità, possiamo considerare come 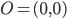 e
e 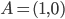 , sono tutti quelli ottenibili come soluzioni di equazioni di grado al più 2 a coefficienti razionali.
, sono tutti quelli ottenibili come soluzioni di equazioni di grado al più 2 a coefficienti razionali.
Questa osservazione dovrebbe darci la caratterizzazione dei punti ottenibili con riga e compasso che è l'obbiettivo di questo articolo.
Vediamo che in effetti le osservazioni 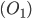 e
e 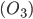 sono in linea con questa tesi; in particolare la risoluzione di
sono in linea con questa tesi; in particolare la risoluzione di 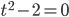 permette di ottenere proprio la coordinata
permette di ottenere proprio la coordinata 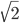
Per dimostrare questa tesi osserviamo a che cosa corrisponde tracciare rette e circonferenze nel piano.
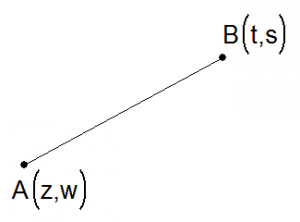
Dati due punti noti del piano, tracciare una retta corrisponde a determinare una equazione di primo grado:
In particolare considerando la formula generale della retta 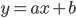 e sostituendo le coordinate per i due punti indicati, si ottiene il sistema:
e sostituendo le coordinate per i due punti indicati, si ottiene il sistema:
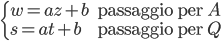
che fornisce un'equazione, di primo grado, nelle incognite x e y della retta del piano passante per A e B.
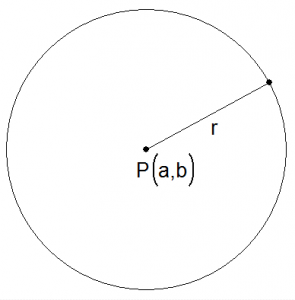
A sua volta tracciare una circonferenza come quella indicata in figura:
Significa trovare il luogo di tutti i punti situati a distanza 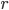 dal punto
dal punto 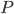 di coordinate
di coordinate 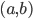 . Ricordiamo di sfuggita che
. Ricordiamo di sfuggita che 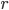 deve essere uguale alla distanza fra due punti noti. L'equazione che si ottiene è:
deve essere uguale alla distanza fra due punti noti. L'equazione che si ottiene è:
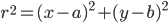
che è un'equazione di secondo grado nelle incognite x e y.
A che cosa corrisponde quindi l'intersezione di una retta e di una circonferenza? Alla soluzione di un sistema di equazioni di primo e secondo grado.
Iterando le costruzioni, ciò che si ottiene è che i punti raggiungibili sono quindi determinati dalla risoluzione di equazioni di grado 2 o multiplo 2.
A questo punto ci rimane soltanto di rimettere insieme i pezzi del discorso per mostrare come questo fatto impedisce che possa essere trovata, con riga e compasso, la costruzione del segmento che duplichi il cubo.