Sane detexi

Forse non si può dire che la notizia abbia raggiunto moltissime persone ma, fra i relativamente pochi che ne sono entrati in contatto, la maggioranza se non la totalità di quelli che avevano anche gli strumenti per collocarla nel giusto contesto di riferimento, ne sono stati colpiti in modo pesante, con coinvolgimenti che si sono fatti sicuramente sentire persino sul piano emotivo.

La notizia è questa: l'università cinese di Tuoxié ha pubblicato una relazione, per altro molto scarna, contenente i risultati preliminari di un progetto (che, tra l'altro, aveva tutt'altre mire) in cui viene segnalato, quasi di sfuggita, che sono state trovate quaterne di numeri interi che violano il grande Teorema di Fermat. Addirittura non una sola quaterna ma una intera classe di quaterne. La pubblicazione stessa è strana perché dopo una succinta descrizione dell'argomento e una quasi inesistente traccia del metodo seguito, termina con un certo numero di pagine che contengono centinaia di QRCode. In ognuno di questi QRCode sono rappresentate semplicemente delle cifre numeriche. Ognuno dei quattro gruppi di QRCode, una volta "espanso" costituisce la rappresentazione di un numero (di circa 50.000 cifre). E questi numeri sono laconicamente esibiti come prova della confutazione del teorema (più e meglio di qualsiasi spiegazione del procedimento utilizzato per ottenerli).

Ricordo rapidamente in che cosa consiste il grande Teorema di Fermat: consiste nell'affermazione seguente:

data l'equazione , non esistono interi tali che l'equazione ammetta soluzione per .

Ora ciò che l'università di Tuoxié sembra indicare è che una quaterna di numeri interi con queste caratteristiche, cioè 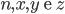tali da soddisfare 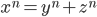sia effettivamente stata trovata. Da qui l'asciuttezza del limitarsi a mostrare i numeri stessi.

E Andrew Wiles?

Già, perché l'affermazione di cui sopra, non è una semplice congettura, cioè un'affermazione che la comunità matematica pensa sia vera ma senza prove conclusive né a favore della sua verità, né della sua falsità. Celebri congetture matematiche sono:

1. Congettura di Golbach: ogni numero pari > 2 è dato dalla somma di due soli numeri primi
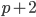2. Congettura dei numeri primi gemelli: esistono infiniti numeri primi tali che anche è un numero primo
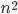3. Congettura di Legendre: per ogni numero esiste sempre un numero primo compreso fra e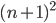

(Ho scelto tre congetture facilmente enunciabili...)

Nel caso del Grande Teorema di Fermat, parliamo di un'affermazione dimostrata. E non dimostrata da Fermat stesso, come ha ritenuto quando scrisse:

"Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitatem non caperet"

cioè: "della qual cosa ho positivamente trovato una mirabile dimostrazione, che però non starebbe nell'esiguità di questo margine di pagina". La dimostrazione è arrivata secoli dopo, ad opera di Andrew Wiles e in modo non privo di colpi di scena (come descritto, ad esempio, in S. Singh - L'ultimo teorema di Fermat - BUR).

Ma allora dove sta il problema?

Si potrebbe facilmente (forse troppo facilmente) prendere per buona questa affermazione, come molti pare abbiano già fatto. Il che non è poi dissimile da quando, alcuni anni fa', sono stati pubblicati e ampiamente commentati dei risultati di esperimenti che avrebbero dimostrato la superabilità della velocità della luce. Anche in quest'ultimo caso c'è già stato chi si è lanciato addirittura nell'immaginare che i risultati cinesi permetterebbero di dimostrare l'esistenza di una fascia di numeri interi talmente grandi che l'immaginazione umana non riesce a rappresentarseli, in cui le leggi matematiche ipotizzate e dimostrate per i numeri di cui il nostro cervello può avere contezza se non proprio intuizione, abbiano una validità più limitata. In un articolo si parlava persino di una "Valle di Tuoxié", intendendo con questo una fascia di numeri (con miliardi o miliardi di miliardi di cifre), in cui le leggi matematiche avrebbero una validità inferiore o diversa. Quasi una sorta di valle incantata in cui numeri interi si ribellerebbero alle leggi matematiche previste, dimostrate e verificate "nel piccolo" come dinosauri che si fossero ribellati, sopravvivendo, alla loro estinzione di massa.

Ma questo fatto non aprirebbe una crepa nell'idea stessa di matematica: aprirebbe una voragine destinata a inghiottirne l'intero edificio. Perché sarebbe come dire che il principio di induzione, per se la proprietà 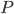vale per 1 e se posso dimostrare che se 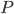vale per allora deve valere necessariamente anche per 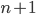, allora 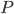deve valere per tutti i numeri interi, non ha davvero più valore; sarebbe uno shock incomparabile con ogni altro, per i matematici che sono abituati a pensare alla propria come all'unica (ultima) disciplina del sapere umano che proceda solo per accumulazioni irrefutabili).

Da qui gli studi che sono già partiti di impostare gli stessi calcoli in altri centri di ricerca indipendenti. In particolare l'unica difficoltà "tecnica" è sviluppare modalità per trattare numeri di circa 50.000 cifre, elevati a esponenti altrettanto smisurati, ottenendone quindi numeri davvero complessi da gestire e computare. Purtroppo però il primo di questi studi di controllo (e questo fatto non può che avere rallentato la velocità degli altri studi paralleli, in cui è da ipotizzare, sono stati quadruplicati sforzi e verifiche), ha incredibilmente confermato la correttezza dei risultati pubblicati dall'università cinese. Pare che effettivamente quei quattro numeri, pur di fronte allo stupore della comunità matematica, soddisfino l'equazione.

Un'altra possibilità

Una possibilità di uscire dallo sconforto è ipotizzare, come già qualcuno sta facendo, che anche la seconda "batteria" di calcolatori si sia imbattuta in un errore (apperentemente deterministico) che non dica nulla sul teorema di Fermat in sé o su altre proprietà dei numeri interi. E il problema non consisterebbe quindi nei numeri in sé ma in qualche tipo di "vizio" o di "varianza" nelle modalità di calcolo.perché, di fatto, non esiste altro modo di verificare il risultato che non sia quello di istruire calcolatori per ripetere gli stessi calcoli e verificarne i risultati.

L'ipotesi che potrebbe salvare capra e cavoli, per altro ancora estremamente vaga, è che i calcoli con numeri di questa grandezza, portino con sé, da qualche parte, degli errori; e che questi errori (qui sta la speranza ma anche l'attuale debolezza dell'ipotesi) si ripetano per qualche ragione sempre nello stesso modo, causando una "correzione" sempre nello stesso senso. Certo non si tratta ancora né di una teoria convincente, né di una affermazione perfettamente definita. Perché non si tratta di avere almeno indizi sul perché certi calcoli falliscano, ma proprio il contrario. E se è vero che un calcolo, a seguito di uno o più errori commessi nel processo, ha un numero enorme di possibilità di fallire, le possibilità che invece, a causa di ulteriori errori, il calcolo non fallisca ma dia sempre il risultato atteso, sono, di contro, del tutto irrisorie.

Significativamente l'unica opzione che non è ancora stata presa seriamente in considerazione è una ulteriore verifica della correttezza del teorema di Fermat-Wiles e della sua dimostrazione.

Piccola nota per il lettore

La notizia sopra è inventata di sana pianta. Perdonami la malignità di non averlo chiarito fin dall'inizio. Volevo esporre un'ipotesi, con un minimo di pathos aggiuntivo; e invitarti a riflettere su che cosa significa dimostrare un teorema e su quali sono le sue conseguenze.