Riprendiamo il ragionamento partito dal che cosa mai potremmo dirci se potessimo parlare con eventuali intelligenze aliene che un giorno volgessero il loro occhio su di noi -oppure sulle quali fossimo per primi noi a rivolgere il nostro. E spostiamo la nostra attenzione non tanto sul che cosa dirci (cioè quali concetti veicolare) ma sul come poter comunicare (cioè come permettere che una qualsiasi comunicazione di concetti possa avere luogo).
Da un lato, sembra facile convincersi che i numeri, in quanto elementi sufficientemente semplici, significativi ed astratti, siano la prima fonte di informazioni. Ogni altro concetto, non esprimibile semplicemente tramite numeri, richiederebbe la conoscenza della biologia e/o della storia evolutiva della popolazione presso cui il concetto ha valore. D'altro canto, tuttavia, non è altrettanto semplice capire come i numeri stessi possano essere trasmessi.
Ad un primo ingenuo approccio si potrebbe credere che qualsiasi entità numerica l'uomo sia stato in grado di definire e rappresentare possa essere utilizzata in una comunicazione. In realtà questa duplicità di aspetti (quanto i numeri siano in stretta relazione con concetti fisici più o meno universali e come noi convenzionalmente li rappresentiamo) complica non di poco l'utilizzo che dei numeri può essere fatto, in quanto veicolo puramente oggettivo di informazioni.
Un importante matematico tedesco dell'800, Leopold Kronecker (che ha fatto qualcosa di più che inventare il Simbolo di Kronecker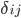 
...), sosteneva:
Dio fece i numeri interi; tutto il resto è opera dell'uomo
Ecco, magari proprio opera nostra sarebbe eccessivo. Ma sicuramente gli enti matematici rappresentativi dei concetti quali numeri razionali, reali, complessi, ecc. ammettono relazioni con i concetti del mondo reale, meno immediate di quanto possano invece ammettere i numeri interi.
Per fare un esempio: in aritmetica la classificazione dei numeri interi come rappresentazione di fenomeni discreti è immediata. Dato un qualsiasi insieme finito di oggetti, pesci, piante,... il numero che li conta non richiede una spiegazione difficile, tanto è vero che viene già acquisita e digerita dai bambini in età prescolare e da un certo numero di animali, pur su un insieme ridotto. Ad esempio ci sono certi uccelli e certi mammiferi per i quali è stato verificato sperimentalmente che conoscono la differenza fra i numeri 1, 2 e 3. Per la cronaca gli esperimenti atti a provarlo avevano la struttura seguente: "Se vedi tre bastoncini arriva cibo, se ne vedi due arriva una punizione." Chi impara a prevedere, fra figure altrimenti identiche, la differenza costituita esclusivamente nel numero degli elementi, allora mostra di saper contare.
Dall'altro lato, anche se è vero che i numeri complessi sono una rappresentazione estremamente efficace e produttiva di concetti chiari e determinati (non vaghi o nebulosi) come le rotazioni del piano, il livello di convenzionalità della loro rappresentazione non è banale.
Consideriamo ad esempio le due rappresentazioni più comuni dei numeri complessi:
- Rappresentazione algebrica:
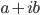con 
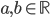e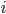 
unità immaginaria; - Rappresentazione esponenziale
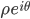con 
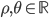e 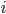unità immaginaria;
Quale delle due riusciremmo a utilizzare senza troppa fatica in una comunicazione da o verso intelligenze aliene? La risposta non è confortante: nessuna se non sono state preventivamente condivise le informazioni seguenti relative alla modalità di rappresentazione:
- Segno grafico che rappresenta un numero (quindi non successione di impulsi discreti);
- Campo numerico dei numeri reali a cui il numero può appartenere (come sanno gli studenti universitari, serve una settimana buona di lezione per dare la definizione di numero reale...);
- Segno grafico che rappresenta una somma o una moltiplicazione (questo secondo segno, nella rappresentazione algebrica usuale, viene persino sottinteso...);
- Concetto di elevamento a potenza;
- Numero di Nepero
; - Unità immaginaria ;
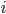- Concetto di rotazione definito, nella convenzione usata dalla notazione esponenziale, usualmente tramite la lettera
- ...
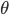
Qui mi fermo ma sono sicuro di essermi dimenticato molti elementi; in altri termini: sono sicuro di aver dato per autoevidenti concetti che invece sono rappresentati solo a mezzo di una convenzione. Lo scopo della lista era solo quello di rendere più esplicito quanti siano i sottintesi che ci permettono di veicolare, tramite una scrittura compatta che si appoggia a un certo numero di convenzioni di scrittura, concetti non proprio elementari.
Bastano i numeri naturali a toglierci dagli impicci?
Ripieghiamo allora sui numeri naturali, quelli che rappresentano cardinalità di insiemi discreti e che quindi richiedono meno convenzioni. La domanda che ci si può porre è: anche nella rappresentazione degli interi ci sono convenzioni? Purtroppo molte più di quante potremmo pensare. Vediamo perché.
Gli antichi grechi avevano sviluppato una matematica raffinata e avevano compreso fin dall'antichità il concetto di numero irrazionale. Eppure pochi fanno mente locale sul fatto che non utilizzavano la nostra notazione numerica (di origine araba o indiana). Utilizzavano una numerazione additiva (la nostra è posizionale) in cui i simboli rappresentavano l'ordine di grandezza e la loro ripetizione significava "quanti elementi per quell'ordine di grandezza". Così, ad esempio: 123 (che sta per un centinaio, due decine e tre unità) si poteva scrivere (nella rappresentazione in uso nell'Attica) come:
- Il simbolo rappresentante le unità, ripetuto tre volte (poniamo di usare il trattino verticale | )
- Il simbolo rappresentante le decine, ripetuto due volte (poniamo di usare il trattino - )
- Un simbolo rappresentante le centinaia (poniamo di usare la T )
- Ne verrebbe fuori una notazione come |||--T (oltretutto l'ordine di in cui vengono scritti non è essenziale; notazioni come T|||-- oppure T--||| rappresentano lo stesso numero).
Lo scopo di questa breve descrizione è relativizzare il concetto: persino nei numeri interi uno stesso numero (ad esempio: centoventitre) può essere scritto in una varietà di modi differenti, nessuno dei quali è particolarmente più naturale o evidente degli altri.
| Notazione | Espressione |
|---|---|
| Numeri arabi, decimale, posizionale | 123 |
| Greca (attica), decimale, additiva | |||--T |
| Numeri arabi (estesi con le maiuscole latine da A a F), esadecimale, posizionale | 7B |
| Numeri arabi, binario, posizionale | 1111011 |
L'impressione data dalla tabella (che contiene un campione molto ristretto di possibilità di esprimere un numero intero) è comunque quella di una grande varietà di rappresentazioni possibili. Non rimane che puntare qualche euro sull'ultima espressione, come quella che più facilmente potrebbe essere compresa, non fosse altro che per la ragione che la notazione binaria è quella più basilare, fra quelle posizionali, dato che utilizza soli due "caratteri" (con un solo "carattere" non si può avere una notazione posizionale). Vediamo nel paragrafo successivo perché anche questa scommessa... sarebbero persa.
Ci possono allora aiutare i numeri binari?
Eppure nemmeno la notazione binaria ci scampa da tutti i guai, perché sarebbe sì abbastanza facilmente interpretabile, ma richiederebbe espressioni estremamente onerose (in termini di lunghezza o indifferentemente di energia necessaria alla trasmissione) per veicolare numeri relativamente modesti.
Oltretutto quale sarebbe il valore comunicativo di una comunicazione espressa in impulsi binari? una volta che riuscissimo a inviare segnali che rappresentino interi, che cosa ci sarebbe, oltre al fatto di aver detto: "Stiamo comunicando" che verrebbe trasmesso?
Archiviato il concetto della difficoltà di trasmissione, vediamo nel prossimo articolo un'ipotesi di invio di informazioni con un significato leggermente più evoluto.