Dopo aver accennato, nell'articolo precedente, alla prima costante di Feigenbaum, vorrei ora dilungarmi sulla sua natura, spiegando meglio in che cosa consista. Il modo migliore che conosco per farlo è simile a quello che ha mia mamma mentre spiega ai miei figli che cosa siano i biscotti, facendoglieli impastare. Ecco: con OpenOffice in questo articolo impasteremo funzioni "tre volte derivabili" e con un massimo locale in [0,1] per capire da dove salta fuori la prima costante di Feigenbaum.
Partiamo dalla prima, la Mappa Logistica
Ipotizziamo di avere una funzione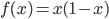 
. Al di là del nome storico di "Mappa Logistica", ciò con cui abbiamo a che fare è semplicemente una parabola. Per di più, con nozioni basilari da Liceo Scientifico, sappiamo che è una parabola con concavità rivolta verso il basso (infatti il coefficiente del termine di secondo grado è negativo) e che intercetta gli assi nell'origine (termine noto nullo). Dato che la derivata prima è 
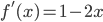e che 
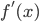si annulla per 
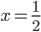, sappiamo che questa funzione è tre volte derivabile (dato che è un polinomio) e che ha un unico massimo locale in [0,1] (per quanto visto prima).
Bene: ha tutte le caratteristiche richieste per poter essere utilizzata; ipotizziamo ora di considerare un qualsiasi numero fra 0 e 1 e di applicare a questo numero (che chiameremo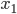 
) la nostra funzione, a meno di un coefficiente 
.
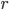Dal punto di vista della formula, potremo scrivere:
.
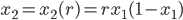Fissato un determinato 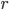che cosa si ottiene continuando indefinitamente a iterare l'applicazione della funzione 
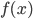? Si ottiene che, per 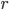sufficientemente piccoli, se mi si perdona l'imprecisione del discorso, l'iterazione della funzione porta a un ben determinato valore limite. Per di più: questo limite può essere soddisfacentemente approssimato tramite un qualsiasi foglio di calcolo.
Consideriamo di porre infatti sulla nostra prima cella (normalmente identificata come A1), il nostro primo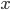 
, cioè l'
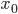iniziale. Non è molto importante quale valore inserire, dato che ciò che ci interessa è vedere il valore limite del processo, non quello iniziale.
Nella nostra cella B1 (a destra della precedente), mettiamo il nostro valore di 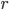, e sugli ulteriori elementi della prima colonna (A2, A3, ecc.), mettiamo una scrittura come questa:
- in A2 avremo =$B$1*(A1*(1-A1))
- in A3 avremo =$B$1*(A2*(1-A2))
- e così via
Per rendere più immediatamente visibile il risultato, potremo immaginare di utilizzare molte celle (ad esempio: un migliaio) e di tracciare, partendo da queste, un grafico a dispersione.
Che cosa otterremmo? Innanzitutto potremmo vedere che il valore scelto inizialmente influenza la parte iniziale (più a sinistra) del grafico, ma influenza molto meno la parte a destra (il valore "tendenziale"). Infatti, qualsiasi valore immaginiamo di porre come primo valore (cella A1) le successive iterazioni della funzione producono una sorta di "oscillazione smorzata" dei valori limite, che tendono ad essere indipendenti dal valore iniziale. Un po' al contrario del detto:
"Chi ben inizia è a metà dell'opera!"
Qui vale più l'altro detto:
"Tutte le strade portano a Roma."
Se variando il valore della cella iniziale i risultati "finali" non variano, possiamo a questo punto chiederci come cambiano i risultati variando il valore del nostro parametro 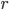. E qui la risposta diventa davvero interessante perché, almeno inizialmente, per piccole variazioni di 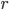si ottengono piccole variazioni del valore limite.
Per un valore di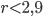 
otteniamo un valore limite sempre crescente; ovviamente nei limiti di poter avere solo una valutazione qualitativa e non certo un calcolo vero e proprio con il nostro foglio di calcolo).
Ma quando questo valore supera di poco il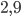 
, la situazione cambia in modo imprevisto: per 
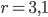, ad esempio, ottengo che la funzione non tende (se applicata infinite volte a se stessa) a un solo valore limite, ma a due valori, in particolare tende a: 0,764570 e 0,558010. Se infatti applichiamo la nostra formula si ha proprio:
.
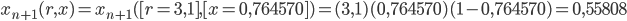così come:
.
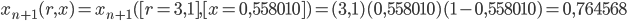Quindi, negli ovvi limiti dell'approssimazione, otteniamo che 0,764570 e 0,558010 sono i due valori fra cui l'applicazione (fissato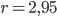 
) permuta per un numero di iterazioni sufficientemente grande.
Questi due valori possono essere intuitivamente concettualizzati come due magneti attorno a cui si dispone via via la limatura di ferro. Dopo un tempo sufficientemente lungo (cioè: iterando un numero adeguato di volte la funzione per un 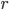fissato) sappiamo che l'ennesimo risultato sarà sufficientemente vicino a uno dei due numeri limiti, anche se, a priori, non possiamo assolutamente predire a quale! In Teoria del Caos due numeri con questa caratteristica vengono definiti attrattori.
Aumentiamo nuovamente ...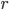
Ma che cosa succede aumentando ulteriormente il valore di 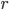? di nuovo i due valori limite variano (in particolare possiamo vedere come, al crescere di 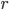si allontanino l'uno dall'altro) fino a un nuovo punto (attorno a 3,455) in cui invece di avere due valori limite, ognuno di questi si sdoppia e otteniamo quattro valori limite.
In particolare per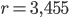 
i valori limite sono approssimabili come:
- 0,838950
- 0,861340
- 0,413230
- 0,467490
Di più: possiamo anche dire che l'ordine con cui uno permuta nell'altro è il seguente:
0,838950 --> 0,467490 --> 0,861340 --> 0,413230 --> 0,838950 e così via.
Aumentando di nuovo il valore di 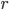ciò che si ottiene, euristicamente, è che il successivo punto in cui i valori limite raddoppiano, si trova attorno a 3,55. E così via con una cascata di ulteriori raddoppi.
Interpretazione pratica della prima costante di Feigenbaum
Ripartiamo da alcuni dati che abbiamo rilevato durante il nostro esperimento in silico.
- Per un valore di
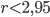la funzione tende a un unico valore limite; - A partire dal valore di
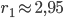(circa: stiamo compiendo grandi approsimazioni); il valore limite si "sdoppia" in due valori differenti, permutanti uno nell'altro ad ogni successiva iterazione. - Arrivati a
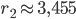di nuovo c'è un raddoppio dei valori limite, che diventano 4. - Qui entra in gioco finalmente la prima costante di Feigenbaum: come possiamo prevedere per quale ulteriore valore di 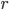, che chiameremo
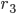si assisterà a un nuovo raddoppio del numero dei valori limite? La regola da applicare è semplice: il rapporto fra 
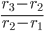è costante ed è proprio la prima costante di Feigenbaum, che vale, per la mappa logistica: δ = 4,66920160910299067185320382 - Come possiamo verificare (non certo dimostrare: solo verificare euristicamente nella nostra "preparazione di biscotti") questa affermazione? La verifica è semplice: calcoliamo dove si dovrebbe trovare il prossimo punto di biforcazione. Da
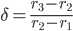si ha che: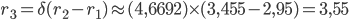 
Negli evidenti limiti della nostra approssimazione, il risultato è in accordo con quanto abbiamo ricavato empiricamente.
Che cosa c'entra il caos?
Una domanda potrebbe sorgere spontanea: ma che c'entra il Caos con questo ragionamento? Per rispondere correttamente forse non è inutile ripartire da una definizione, cioè quella di Caos. Una bellissima ma un tantino ostica risposta la si può trovare qui. Che dire? Dice tutto; ma forse a noi, per intenderci, basta anche un po' meno...
Potremmo infatti lavorare solo sull'intuizione dei concetti invece che sulla loro espressione rigorosa e dire:
"Un sistema non è caotico quando a una minima variazione delle condizioni iniziali, segue una minima variazione delle condizioni finali; un sistema è caotico quando minime variazioni portano a enormi differenze nelle condizioni finali."
Ha attinenza questo con l'idea di caotico=non deterministico? Sì, anche se potrebbe sembrare una sorta di far rientrare dalla finestra ciò che abbiamo fatto uscire dalla porta. Perché per noi caotico implica: data una minima variazione otteniamo risultati non calcolabili. E soprattutto, potremmo dire: quando gli attrattori sono più di uno, spostarsi di poco dall'intorno di uno di questi attrattori, potrebbe comportare il capitare nell'intorno di un altro. E la distanza fra i due è una distanza discreta e determinabile, mentre non è a priori determinabile nell'intorno di quale attrattore ci si possa venire a trovare.
Quando poi gli attrattori fossero 
si vede bene come la possibilità di determinare la posizione esatta (qualunque cosa posizione significhi nella nostra analisi della funzione...) diventa sempre più arduo.
Portando un discorso verso un concetto più concreto: immaginiamo una certa configurazione che in un certo istante ci rappresenta il sistema dinamico delle masse d'aria presenti in un'atmosfera. Immaginiamo che la funzione che vogliamo studiare rappresenti l'evoluzione del tempo atmosferico nel tempo. Qui il concetto diventa molto più chiaro: se a piccole variazioni (non prevedibili) conseguono perturbazioni notevoli del sistema dinamico (tipo: uragano o calma piatta), il sistema è caotico. E la previsione non è possibile. Se invece esistessero modalità di determinare l'indice implicito di caoticità del sistema, potremmo anche fornire non solo una previsione del tempo ma anche un indice statistico di affidabilità della previsione stessa.
Cosa che, di fatto, avviene quando insieme alla previsione, viene fornita anche la sua implicita affidabilità.