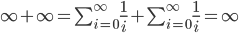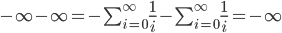...quello che l'uomo comune manda "al diavolo".
Si tratta di una massima della mia professoressa universitaria di Algebra Astratta. Con questo articolo vorrei mostrare perché nell'articolo sulla legge di Titius-Bode non sono riuscito a scrivere 
ma ho dovuto scrivere 
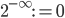. La differenza apparentemente è data solo dal segno 
("due punti"). Ma dietro questo semplice segno, ci sono significati inconciliabili.
Convenzioni di rappresentazione
Partiamo innanzitutto dal chiarire in che cosa consista la differenza fra le due notazioni.
Che cosa significa ? Significa che esiste un insieme numerico che comprende anche l'elemento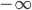 
; che questo elemento può essere utilizzato almeno in una espressione che coinvolge l'elevamento a potenza. E che, nell'espressione sopra riportata, si ottiene zero.
Detta così, pare una richiesta piuttosto impegnativa...
Che cosa significa, invece, 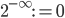? Il segno di che precede il segno 
indica una cosa completamente differente.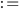 
significa, comunemente nella notazione matematica, uguale per definizione. La lettura della seconda espressione suona quindi così: "Poniamo di utilizzare un elemento rappresentato con il simbolo 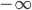; e poniamo, per definizione, che valga la relazione 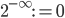". In questo caso stiamo solo parlando di "convenzione" e di "notazione di comodo".
Ma da dove nasce questa prudenza nell'utilizzo dell'infinito?
Estendere i campi numerici
Molti di noi, alla scuola superiore, hanno studiato l'estensione dei numeri naturali con i numeri relativi, o con i razionali, o con entrambi, ecc. In tutte queste estensioni, vigevano, anche senza che ce ne rendessimo ben conto, due regole abbastanza semplici:
- L'insieme ottenuto a seguito dell'estensione era chiuso rispetto alle operazioni prese in esame; cioè potevo prendere qualsiasi numero (poniamo: intero relativo) e applicarvi la somma e il suo inverso, la sottrazione, ottenendo come risultato ancora un numero intero relativo; in breve:
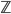(l'insieme dei numeri interi relativi) è chiuso rispetto a 
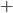. In effetti anche 
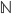era chiuso rispetto a 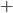tuttavia non esisteva l'elemento opposto. - Il vantaggio dell'estensione risiedeva nel fatto che certe operazioni, impossibili nell'insieme più ristretto, diventavano invece possibili in quello esteso. Ad esempio: i numeri interi relativi sono introdotti molto naturalmente come estensione dei numeri naturali per ottenere di estendere la sottrazione anche nel caso che il numero da cui si vuole sottrarre (minuendo) sia inferiore al alla quantità che si vuole sottrarre (sottraendo). Nell'insieme numerico 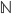dei numeri naturali l'operazione:
non è possibile mentre nell'insieme 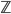si può scrivere: 
dato che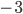 
è un numero intero relativo.
Un altro esempio che gode delle stesse "condizioni al contorno" è l'introduzione dei numeri razionali a partire dagli interi relativi per "estendere" la moltiplicazione. Anche qui è il problema dell'inverso rispetto alla moltiplicazione a trovare un completamento: senza i numeri razionali, le uniche divisioni possibili erano quelle in cui il dividendo era multiplo del divisore.
Perché allora dobbiamo adesso farla tanto difficile con l'introduzione dell'infinito? Non basterebbe semplicemente aggiungerlo per chiudere operazioni come l'elevamento a potenza?
Purtroppo no... Vediamo in dettaglio per quali ragioni.
Definizione dell'infinito
L'infinito come numero, al di là di saperlo rappresentare facilmente col noto simbolo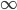 
, non è altrettanto facile da definire. Ad esempio, fra tutte le definizioni di infinito che si possono dare, a me piace molto questa:
Un insieme è infinito se e solo se può essere messo in relazione biunivoca con una sua parte propria.
Ad esempio: sono più i numeri naturali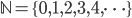 
oppure i numeri pari 
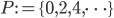? La risposta è piuttosto sorprendente: 
; e questo è vero in quanto sono insiemi infiniti e in quanto esiste una relazione biunivoca che associa ogni elemento di 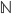a ogni elemento di 
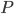. In particolare la relazione è data dall'ovvia funzione "raddoppio": 
data da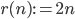 
.
Questa definizione, tuttavia, non ci aiuta nel nostro problema. Cerchiamo di ricorrere a una definizione più operativa. Nonostante ci siano moltissimi modi per definire il concetto e per "gestirlo", potrebbero essere molto comode le serie numeriche. Consideriamo le due somme seguenti:
Se immaginiamo di estendere le somme a tutti gli infiniti addendi dati dalla ovvia formula generale, otteniamo:
-
Questa serie prende il nome di Serie armonica. -
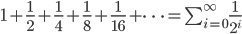Questa serie prende il nome di Serie geometrica
In entrambi i casi il termine generale decresce; ma nel primo caso la somma di tutti gli addendi è 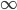(i matematici direbbero: "la serie diverge") mentre nel secondo caso è un numero finito, in particolare 2 (in rete ci sono molte dimostrazioni di questa affermazione.)
Consideriamo quindi che l'infinito sia, in atto, quello che le serie divergenti sono in potenza. Già qui ci accorgiamo che diverse serie possono divergere avendo termini generali completamente differenti; tuttavia divergeranno tutte a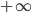 
o 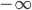senza poter distinguere quale fosse il termine generale originario.
Immaginiamo quindi di considerare la serie armonica come una delle serie generatrici del nostro infinito. Sicuramente possiamo affermare:
ci possiamo anche spingere a dire:
come pure:
ma che cosa dire di:
?
Un primo spunto potrebbe venire da questa considerazione:
Ma se
allora non potrei semplicemente riordinare tutti i termini e ottenere
e ottenere così un bel
?
La risposta purtroppo è: no. Non è possibile riordinare questi termini. La proprietà commutativa che funziona, quando sommiamo numeri reali, per un numero finito qualsiasi di addendi, non è detto che continui a valere quando sommiamo infiniti addendi.
Esiste in proposito un bellissimo teorema, che relativizza di molto il nostro concetto intuitivo di commutatività. Consideriamo, per introdurlo, una leggera variante della serie armonica: la serie armonica a segni alterni. Consideriamo cioè la serie data da:
Di questa serie si può dimostrare che:
- è una serie convergente
- la sua somma è
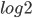
Questa serie ha inoltre una ulteriore caratteristica: non solo converge (converge semplicemente), ma la serie in cui consideriamo come termine generale il valore assoluto del suo termine (cioè la serie armonica) diverge. Quindi: la serie converge semplicemente ma non assolutamente.
Con queste condizioni il teorema di Riemann Dini dimostra qualcosa di notevolissimo: è possibile riordinare opportunamente gli elementi della somma per ottenere:
- che la serie ottenuta converga a qualsiasi numero prefissato;
- che la serie diverga!
Questo ci porta a dire che la commutatività (nelle condizioni del teorema di Riemann Dini) è qualcosa di assolutamente non valido nella somma di infiniti addendi. Detto per inciso, anche questo teorema può essere utilizzato per definire, a ritroso, l'infinito come:
Un insieme
è infinito se e solo se riordinare la somma di una serie indicizzata da
) porta a ottenere risultati differenti in accordo con il teorema di Riemann Dini.
Certo non è una definizione molto diretta e semplice; ma appena ci si rifletta un attimo, è piuttosto affascinante.
Conclusione
Oltre che per ridefinire l'infinito, il teorema appena visto ci serve, allo stesso modo, per dichiarare come indefinita l'operazione di somma algebrica fra infiniti. La successione dei passaggi logici è infatti:
- Dato 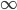è possibile immaginarlo come somma di una serie; immaginiamo di usare la serie armonica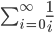
- L'«operazione» può quindi essere rappresentata come ;
- Se fosse possibile ottenere una serie unica riordinando i termini (ad esempio scegliendo un termine dalla prima e un termine dalla seconda), ricadremmo nel teorema di Riemann Dini;
- Ma questo comporterebbe che la somma della serie ottenuta dipenderebbe dall'ordine in cui vengono sommati gli addendi;
- Ma allora può avere come risultato un qualsiasi valore in
; - Quindi: o non è possibile riordinare la serie e quindi non è possibile determinare il risultato dell'operazione (e questo è quanto stiamo sostenendo) oppure la somma della serie ottenuta sarebbe indeterminata in quanto diversa in funzione del riordino effettuato. Ma anche questo secondo risultato concorda nell'affermare che non è ben definita, che è quanto si voleva mostrare.
Appare quindi più cauto considerare di cavarsela con un 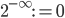piuttosto che parlare davvero di un insieme numerico chiuso rispetto alle operazioni.