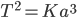Ognuno di noi perde, a volte, qualcosa: le chiavi di casa, un foglio con un appunto importante, la pazienza... Difficilmente però, persino ai più distratti, può mai essere capitato di aver perso un intero pianeta... Eppure ci sono nello spazio un numero sterminato di pianeti non propriamente persi, ma sicuramente: ancora da trovare. Dopo aver visto una interessantissima conferenza (questa) vorrei brevemente raccontare, con qualche semplificazione, come si cerca un pianeta. O, per dir meglio: quali sono le modalità di determinazione dell'esistenza, della dimensione e della massa e della probabile composizione di un pianeta extrasolare.
La missione Kepler
La missione Kepler della NASA è nata con l'obbiettivo di sfruttare un semplicissimo meccanismo per la rilevazione dei pianeti: la diminuzione di luce causata dal passaggio del pianeta fra noi e la stella. Apparentemente sembra un sistema banale (e per certi versi è così). Il difficile è stato semmai avere a disposizione uno strumento sufficientemente sensibile alle variazioni luminose da poter rilevare questo tipo di transiti.
Un elemento che è opportuno ricordare è che, per poter rilevare pianeti, occorre che questi transitino esattamente davanti alla Stella. Se il piano di rivoluzione dei pianeti non fosse allineato alla linea che congiunge la Terra e la Stella in esame, non si potrebbe osservare alcun transito. Ma quindi quante sono le possibilità di rilevare pianeti? Secondo le stime degli scienziati della missione Kepler, questa modalità di rilevamento dei pianeti, per ragioni geometriche, può essere in grado di rilevare un numero compreso fra 1% e 10% dei sistemi planetari effettivamente esistenti.
Quindi: se sono stati trovati circa 2.000 sistemi planetari su 150.000 stelle sotto osservazione, questo significa che circa l'1% delle stelle osservate hanno rilevato un sistema planetario. Ma questo dato è congruente con l'immaginare... che quantomeno le stelle con un sistema planetario siano moltissime, forse addirittura la maggior parte delle stelle della Via Lattea e, per analogia, la maggior parte delle stelle dell'universo.
Ricordiamo per un attimo l'equazione di Drake:
dove:
Numero di civiltà extraterrestri con cui stabilire un contatto
Tasso di formazione delle stelle nella nostra Galassia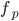
Frazione di Stelle con pianeti (sempre: nella nostra galassia)
Frazione di pianeti in condizione di ospitare vita. Un tempo si riteneva che questo corrispondesse ai pianeti nella fascia di "Goldilocks"; oggi la condizione è più generica, dopo le scoperte su pianeti e satelliti del Sistema Solare con quote significative di acqua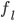
Frazione di pianeti in cui effettivamente si è sviluppata la vita
Frazione di pianeti in cui si sono evoluti esseri intelligenti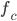
Frazione di pianeti in cui la vita intelligente ha sviluppato sistemi di comunicazione in grado di mettersi in contatto con noi
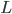Stima della durata delle civiltà evolute.
Dai risultati della missione Kepler sembrerebbe che il valore di 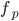sia molto più alto di quanto ritenuto in passato; il team della missione Kepler stima che i pianeti presenti nella nostra galassia siano attorno ai 50 miliardi, di cui almeno 500 milioni nella zona abitabile.
I transiti e la terza legge di Keplero
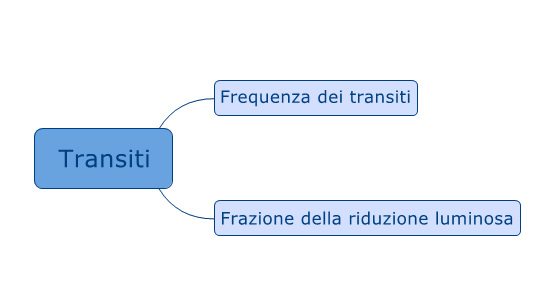
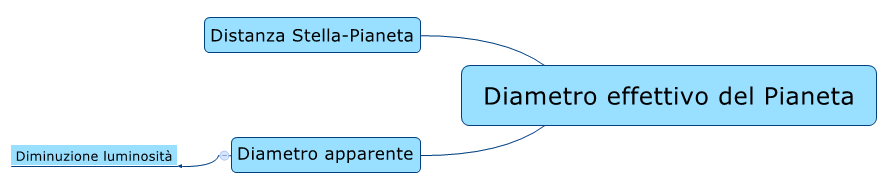
Torniamo quindi ad avere un transito, cioè un passaggio di un corpo di fronte alla Stella ("di fronte": ovviamente dal nostro punto di vista). Questo semplice fenomeno ci può dare informazioni sui seguenti aspetti:
- Dimensione relativa del corpo relativamente alla dimensione della stella
- Frequenza di passaggio del corpo davanti alla stella e, di conseguenza, periodo orbitale.
Ma a questo punto c'è un altro elemento da considerare, un elemento, per intenderci, che ci fa apprezzare appieno l'aggettivo "universale" da applicare alle leggi fisiche. L'elemento è la terza legge universale di Kepler (non è una coincidenza il nome della missione!). la legge afferma che:
I quadrati dei periodi di rivoluzione sono proporzionali ai cubi dei semiassi maggiori delle orbite. In simboli abbiamo:
Per di più, data la legge di gravitazione universale, sappiamo anche precisare quanto valga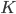 
; in particolare, se la massa del pianeta 
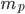è trascurabile rispetto alla massa della stella 
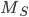cioè se 
allora si può approssimare la terza legge con una versione leggermente più differente:
dove 
è la costante di gravitazione universale.
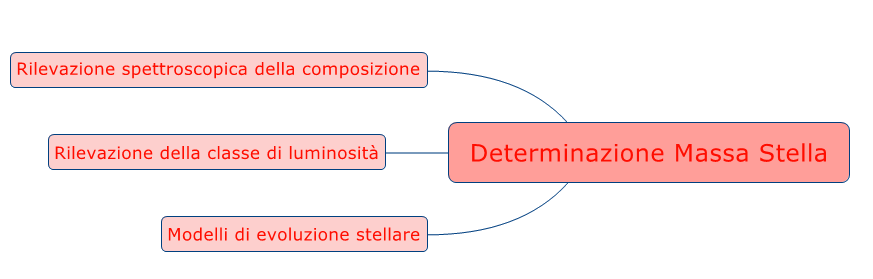
L'ultimo elemento da ricavare per poter usare la formula è quindi la massa stella 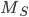. Ma per questo il procedimento prevede:
- determinazione accurata, tramite spettroscopia, della classe stellare.
- determinazione accurata della classe di luminosità;
- Combinando insieme queste due informazioni e partendo dai modelli di evoluzione stellare, si determina la massa della stella.
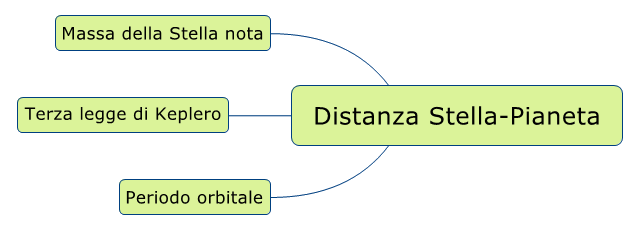
Ma questa formula permette, conoscendo il periodo 
di calcolare la distanza del pianeta dalla Stella tramite:
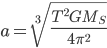
A questo punto tutti gli elementi ottenuti permettono di stabilire la distanza del pianeta dalla stella.
Ma conoscendo diametro apparente e distanza, per ragioni geometriche (di semplice proporzionalità) è possibile determinare anche la dimensione del pianeta. In effetti: una copertura dell'1% della superficie della Stella può essere ottenuto:
- da un pianeta che abbia una dimensione
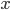a una certa distanza - oppure da un pianeta che abbia dimensioni 10 volte maggiori ma si trovi a una distanza
, cioè 10 volte maggiore dalla Stella stessa.
Che cosa rimane quindi da determinare, per avere un quadro più completo? La massa del pianeta; ma anche per questo c'è una soluzione.
Massa, densità, composizione
Per poter ricavare la massa dei pianeti, la distanza della stella deve essere valutata in due momenti in cui il pianeta si trova in posizioni opposte rispetto alla Stella, vale a dire: durante un transito e a metà del periodo fra due transiti, quando si troverà, per così dire, "dietro" alla stella. Nel primo caso il pianeta "tirerà" la stella verso si sé e quindi verso di noi; ne secondo caso il pianeta, tirando la stella verso di sé, la allontanerà da noi. Negli altri punti dell'orbita le eventuali "oscillazioni" che potessero essere rilevate non sarebbero indicative della massa del singolo pianeta in esame ma di altri fenomeni (altri pianeti, altri corpi in orbita, ecc.).
Queste oscillazioni, di fatto si caratterizzano per una variazione (rilevabile come effetto Doppler) delle righe spettrografiche. Una variazione di questo tipo, se da una parte conferma che la variazione di luminosità della stella è dovuta a un pianeta in orbita, dall'altra è più precisa perché permette di calcolare la massa del pianeta. Infatti la regola generale è che maggiore è la massa del pianeta, maggiore sarà lo spostamento "indotto" dal pianeta sulla stella.
Occorre infatti ricordare che non sono tanto i pianeti a ruotare intorno alle stelle quanto pianeti e stelle a ruotare, a coppie, attorno al centro di massa del sistema. Quando la massa della stella è molto maggiore di quella del pianeta, il centro di massa del sistema non è molto lontano dal centro di massa della sola stella; e sembra proprio che sia il solo pianeta a ruotare. Nel nostro sistema solare abbiamo tuttavia un caso notevole: Plutone e la sua luna Caronte, avendo masse comparabili, hanno un centro di massa esterno a Plutone (che pure rimane il corpo più grande del sistema). Per questa coppia celeste è più evidente che ogni rivoluzione di Caronte è in realtà una danza, molto più complessa, di entrambi.
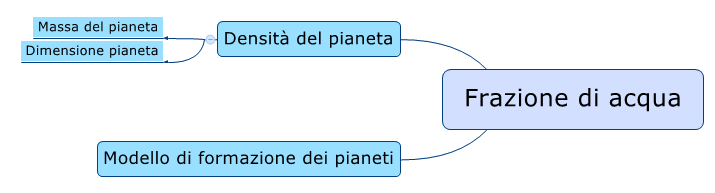
Tornando a noi, una volta noti il volume e la massa, è semplice calcolare la densità. A questo punto gli astronomi hanno tutti gli elementi per stabilire una sorta di classificazione, o, meglio, per attribuire i pianeti scoperti a una delle quattro "classi" seguenti:
- Terre - Pianeti con una massa circa equivalente a quella della Terra (entro le 5 masse terrestri). Nel nostro sistema solare sono "Terre" tutti i pianeti interni: Mercurio, Venere, Terra e Marte.
- Superterre - Pianeti con una massa circa compresa fra 3 e 10 masse terrestri. Nel nostro sistema solare non esistono pianeti di questa classe.
- Nettuniani - Pianeti con masse circa compresa fra 10 e 50 masse terrestri. Esempi nostrani: Urano e Nettuno
- Gioviani - Pianeti oltre le 50 masse solari. Nel nostro sistema solare: Giove (300 masse terrestri) e Saturno (100 masse terrestri). Una particolare classe di questi pianeti sono quelli definiti Hot Jupiters, cioè pianeti di massa gioviana ma con orbite più strettamente ravvicinate al loro sole di quanto non sia quella di Mercurio.
Fra i pianeti delle prime due classi, coniugando le informazioni relative alla densità e alle teorie relative alla formazione dei pianeti per condensazione a partire da nuvole di gas primordiale, si ottengono infine ipotesi relativamente alla composizione. In particolare, quando gli astronomi parlano di pianeti con una percentuale di acqua molto alta, anche fino al 10% (contro lo 0,02% di acqua presente sul nostro pianeta) il percorso logico che è stato compiuto per arrivare a questo tipo di supposizioni è il seguente:
- La massa caratterizza il pianeta come un pianeta di tipo terrestre;
- Questo implica che si tratti di un pianeta "roccioso" e non "gassoso"
- Se la densità (rapporto fra massa e volume) è al di sotto di una certa soglia, allora la percentuale d'acqua dovrebbe essere, di conseguenza, rilevante.
Lo "strano caso" di KIC 8462852
In questa bellissima avventura dell'astronomia e della logica, che cosa poteva appassionare di più gli scienziati, se non l'inaspettato? Giacché se la conferma sperimentale di un'ipotesi teorica appaga, ma la sua confutazione insieme spiazza (siamo uomini) e affascina (è scienza, non credenza!)
E l'inspiegato (chi può dire che sia inspiegabile?) puntualmente è arrivato, sotto forma di una stella, col nome impronunciabile di KIC 8462852 (chiamata anche Tabby's Star, dal nome dell'astronoma Tabetha Boyajian che l'ha per prima indagata), che subisce transiti del tutto fuori scala rispetto allo "standard" degli altri 2.000 sistemi planetari trovati fin qui. Perché la sua diminuzione di luminosità non è dell'ordine dello 0,1% ma ha registrato, nel corso di anni successivi, diminuzioni del 10, del 15 e persino del 20%. Oltretutto per un periodo di tempo non di ore ma di settimane.
Una spiegazione alternativa potrebbe essere che la diminuzione di luminosità è data dalla stella stessa.Ma nessuno dei modelli di funzionamento stellare a oggi noti spiegherebbe questa variazione di luminosità intrinseca, quindi gli astronomi ritengono questa ipotesi la meno probabile.
Che cosa provoca queste diminuzioni apparenti, rilevanti e non prevedibili di luminosità? Quali corpi possono essere sufficientemente estesi da oscurare la luminosità così tanto e così a lungo?
A oggi non abbiamo a disposizione risposte convincenti, ma solo una stupenda domanda.