Sulla distribuzione dei numeri primi

Nel Marzo di quest'anno è stato pubblicato su Nature un articolo che trattava di una particolarità relativa alla distribuzione dei numeri primi. In particolare, analizzando il primo miliardo di numeri primi, venivano fatte considerazioni sulla probabilità che due numeri primi successivi avessero fra di loro una sorta di legame oppure non ne avessero nessuno. Se i numeri primi fossero distribuiti randomicamente, non dovrebbero avere alcun legame; viceversa rilevare "regole" o quantomento "maggiori probabilità" implicherebbe una non perfetta casualità nella distribuzione. In questo articolo descriverò brevemente il risultato ottenuto, insieme ad alcune sue implicazioni.

Descrizione del risultato ottenuto

Partiamo da una brevissima introduzione: i numeri primi superiori al 5 possono terminare esclusivamente con le cifre 1,3,7 e 9. Ci si convince facilmente di questo fatto considerando che: se un numero intero termina per una cifra pari, allora è esso stesso pari e quindi non primo; se termina per 5, è multiplo di 5 e quindi non primo.

L'analisi di Robert J. Lemke Oliver e Kannan Soundararajan ha rilevato invece che, pur a fronte di una distribuzione uniforme dei 4 numeri come ultima cifra (circa il 25% dei primi termina per 1, il 25% per 3, e così via) ciò che invece non è uniforme proviene dall'analisi comparata di due numeri primi successivi: se un primo finisce per 1, quante sono le probabilità che il numero primo successivo finisca per 1 rispetto alle probabilità che finisca per 3, 7 o 9?

Il risultato ha sorpreso i matematici: la probabilità che due numeri primi consecutivi (ovviamente: rispetto all'ordinamento dei primi, non consecutivi come interi) finiscano con la stessa cifra è inferiore alla probabilità che il secondo numero primo finisca con una cifra differente. In particolare, analizzando il primo miliardo di numeri primi, la probabilità che a un numero primo che termina per 1 ne segua un altro che termini ancora per 1 sono solo del 18% (contro il 25% teorico di una distribuzione random). E questo non cambia se si considerano le probabilità che un numero primo che termina per 3 (o per 7 o per 9) sia seguito da un altro numero primo che termini nuovamente per 3 (rispettivamente per 7 o per 9).

 

Accettabilità del metodo

Una frase, tuttavia, suona veramente male nell'articolo:

"The bias persists but slowly decreases as numbers get larger"

Il fatto che questo effetto di legame apparente descresca (lentamente?!) al crescere dei numeri potrebbe fornire indicazioni puntuali se trattassimo con un insieme finito di numeri. Ma qui stiamo ragionando su infiniti numeri, quindi chi ci assicura che questo effetto non tenda semplicemente a zero (e che quindi non sia se non una particolarità dell'intervallo numerico considerato invece che dei numeri primi in sé)?

Faccio un esempio banale: nella prima decina di interi esistono 4 numeri primi: il 2, il 3, il 5 e il 7. Ma questa alta percentuale (40%) di numeri primi decresce "as numbers get larger". Quindi parliamo di una proprietà vera o di un effetto apparente?

D'altro canto l'approccio statistico, pur illuminando con un fiammifero l'immensità della notte, è un brillante tentativo di analisi; ed è innegabile che qualcosa abbia prodotto. Perché, fosse anche una tendenza destinata a dissolversi asintoticamente all'infinito (questo tipo di analisi statistica, per sua natura, non può affermare nulla a riguardo), fornisce comunque un risultato, una direzione verso cui muoversi.

 

Rifacciamo un po' di calcoli...

C'è di più: le valutazioni statistiche di Lemke Oliver e Soundararajan, su intervalli numerici di molti ordini di grandezza inferiori, possono anche essere ottenuti con strumenti di calcolo molto più alla buona, come ad esempio: OpenOffice. Vediamo con quali risultati.

Scarichiamo infatti da internet (ad esempio da qui) la lista dei primi 50.000 numeri primi (cioè i primi compresi fra il 2 e 611.953. Con semplici manipolazioni (converti testo in colonne, taglia incolla fino ad avere tutti i numeri in una sola colonna e riordino dei valori in colonna) otteniamo la lista, ordinata, nella prima colonna di OpenOffice.

Nella seconda colonna possiamo inserire gli stessi numeri ma slittati in alto di una cella, in modo che su due celle adiacenti (in orizzontale) si trovino un numero primo e il suo successore. A questo punto non rimane, con una semplice manipolazione di stringhe, che prendere l'ultima cifra del numero sulla prima colonna, l'ultima cifra del numero sulla seconda colonna e metterle insieme. La colonna così ottenuta contiene le stringhe di due digit la cui frequenza ci proponiamo di verificare.

Ma questa verifica è semplicissima utilizzando le tabelle pivot di OpenOffice e impostando come colonne le nostre sequenze di due digit e come righe il conteggio di queste frequenze.

Ciò che otteniamo, limitando la nostra osservazione alla sola cifra 1 seguita da un'altra cifra (per le altre cifre 3, 7 e 9 il risultato è analogo), è rappresentabile come da tabella seguente:

Sequenza	N° Occorrenze	% sul totale
11	1.978	15,8%
13	4.062	32,5%
17	4.212	33,7%
19	2.235	17,9%

Come si può notare, dopo la cifra 1 non abbiamo la stessa possibilità di trovare 1, 3, 7 o 9 ma le probabilità di avere come ultima cifra 1 sono inferiori a quelle di trovare ogni altra cifra. E lo stesso risultato lo otteniamo con il 3, il 7 e il 9. Mediamente, la possibilità di trovare una cifra ripetuta (nelle condizioni poste sopra) sui primi 50.000 numeri primi è del 15% contro il 25% teoricamente disponibile se i numeri fossero distribuiti in modo assolutamente casuale.

 

Interpretazione del risultato

Ma che significato ha questa minore probabilità, relativamente ai numeri in sé? Partiamo da una trascrizione della frase "numero primo che termina con la cifra 1 seguito dal successivo primo che termina con 1". Poniamo che il nostro primo sia 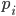e che termini con 1. Se il primo successivo 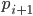terminasse con 1 significherebbe che la differenza fra i due numeri sarebbe un multiplo di 10. Vediamo alcuni esempi di primi successivi che terminano entrambi per 1:

• 181 - 191;
• 241 - 251;
• 349.241 - 349.291;
• ma anche la quaterna di primi consecutivi: 507.421 - 507.431 - 507.461 - 507.491;
• ecc.

 

Possiamo quindi parafrasare il risultato ottenuto dicendo: la probabilità che due primi successivi differiscano per un multiplo di 10 è inferiore rispetto alla probabilità che due primi successivi differiscano per un valore differente.

 

Variazione della rappresentazione numerica

Che cosa succede ora se cambiamo la base numerica di rappresentazione? La domanda ha un senso, tanto è vero che è la domanda che molti commentatori dell'articolo su Nature hanno posto... Infatti la rappresentazione numerica a base 10 che usa le 10 cifre arabe (o meglio, le 9 cifre arabe più lo zero) è fondamentale per osservazioni come quella iniziale sulle quattro cifre finali possibili per i numeri primi. Tuttavia i primi sono tali indipendentemente dalla rappresentazione numerica e altre basi numeriche portano a risultati notevolmente differenti: si pensi anche solo al caso eclatante della notazione binaria: tutti i dispari terminano per 1, quindi tutti i primi superiori al 2 terminano per 1...

Variamo quindi la base numerica, cominciando dalla base 11.

Prima osservazione. Rappresentando i numeri in base 11 (in cui il 10 si scrive A e l'11 si scrive 10 e così via, fino al 21 che si scrive 1A e il 22 si scrive 20, ecc.), le cifre terminali possibili sono: tutte le cifre con l'eccezione dello 0.

Che lo 0 sia da escludere è abbastanza scontato, dato che finiscono per zero tutti i numeri multipli di 11, quindi in particolare non primi. Oltre tutto questa considerazione (esclusione dello zero come ultima cifra dei primi) vale, con analogo ragionamento, per ogni base numerica considerata.

Il fatto invece che ogni altra cifra possa essere la cifra finale di un numero primo è un elemento di novità rispetto alla base 10.

Seconda osservazione. Anche con la rappresentazione in base 11, analizzando i primi 50.000 numeri primi, persiste la regola in base alla quale la frequenza di un numero primo che finisce per la cifra seguito da un altro numero primo che finisce sempre per la cifra è molto più bassa della frequenza randomica (che in questo caso, trattandosi di 10 cifre possibili, dovrebbe essere attorno al 10%).

La tabella seguente illustra meglio il risultato:

Sequenza	Frequenza sul totale delle coppie
11	0,330%
22	0,238%
33	0,262%
44	0,324%
55	0,322%
66	0,328%
77	0,302%
88	0,244%
99	0,230%
AA	0,356%

Se è vero che la probabilità che un numero primo (rappresentato in base 11) termini con una delle 10 cifre possibili è attorno al 10%, le frequenze di coppie 11, 22, ecc. dovrebbero essere attorno all'1%, se distribuite randomicamente, mentre nella tabella si vede chiaramente come sono tutte notevolmente inferiori. La media è dello 0,29% quindi nemmeno un terzo del valore (ipoteticamente) atteso.

Terza osservazione. Nella rappresentazione in base 11, oltre al fenomeno delle coppie "meno probabili" si evidenzia anche il fenomeno opposto: quello delle coppie più probabili. Ad esempio: dopo la cifra 1 ci sono il 2,71% di probabilità che il successivo numero primo, rappresentato in base 11, abbia come ultima cifra il 7. Ma allo stesso modo, incrementando di una unità entrambe le cifre si ottiene la coppia 28, che, a sua volta, il 2,08% di probabilità (contro il valore medio atteso dell'1%). Questa regola vale per tutte le coppie possibili ottenute incrementando di una unità entrambe le cifre. Per di più, nel caso della prima cifra 5, siccome l'ulteriore cifra dovrebbe essere lo 0 ma questa cifra non è ammessa, si osserva che la distribuzione di frequenze e più omogenea per le coppie che cominciano con 5, nel senso che non c'è una cifra con una probabilità così elevata. Anche qui una tabella mostra più immediatamente la questione:

Sequenza	Frequenza
17	2,168%
28	2,078%
39	2,062%
4A	2,116%
50	coppia non ammessa
61	2,074%
72	2,386%
83	2,028%
94	2,388%

In particolare si osserva che la regola (empirica) che produce la maggiore possibilità di ottenere numeri primi successivi è quella per cui l'ultima cifra di un determinato primo (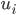) sia legata all'ultima cifra del primo successivo (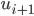) in base alla relazione:

.

 

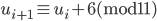Consideriamo ora la rappresentazione in base 12.

Quarta osservazione. Rappresentando i numeri in base 12, le cifre terminali possibili sono esclusivamente 1, 5, 7 e B. Anche per questa rappresentazione, le coppie di ultime cifre meno probabili sono le coppie di cifre ripetute. Più in generale questo comportamento generale si osserva in modo generale. La frase (almeno nell'articolo divulgativo su Nature) è meno precisa e suona come:

almost all gaps are disfavoured

Vediamo in una tabella riassuntiva per le sole basi numeriche da 10 a 15 come si presenta il fenomeno della coppia di cifre uguali "sfavorita"

Base	Coppie uguali	Valore Probabilità
10	0,150	6,250
11	0,029	1,000
12	0,145	6,250
13	0,014	0,694
14	0,075	2,778
15	0,029	1,563

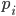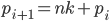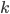Abbiamo quindi visto che, dato un numero primo , il suo successivo ha più probabilità di essere trovato al di fuori dei numeri esprimibili come dove è un generico intero, è la base di rappresentazione usata, quindi .

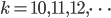Ora la domanda che rimane da porsi è piuttosto la seguente: Questo fatto rilevato statisticamente (non dimostrato come teorema) è una stramba particolarità dei numeri primi o è un altro modo, più arzigogolato, di definire un numero primo?