I due principali poli di attrazione delle dimostrazioni matematiche sono costituiti dall'esibire l'oggetto matematico che si intende dimostrare, attraverso la sua "costruzione" e, dal canto opposto, dal mostrare che negando l'assunto si giunge a un "assurdo". Ovviamente senza escludere dimostrazioni che ricorrano all'uno e all'altro dei metodi.
Ma, se è piuttosto intuitivo comprendere che cosa sia una dimostrazione per «costruzione», la dimostrazione per assurdo innesca concetti piuttosto complessi che, approfondendo l'indagine, appaiono non altrettanto evidenti. Si può affermare ad esempio che costruendo un oggetto si esibisce la prova di quanto si afferma, direttamente all'interno delle regole e delle definizioni entro i quali ha senso. Diversamente, nella dimostrazione "per assurdo" si pone come assunto un'affermazione opposta a quella che si vuole dimostrare, cercando di ottenere una contraddizione nel ragionamento. E questo implica che ci si appoggerà, per la dimostrazione, a un sistema di riferimento logico più forte che va necessariamente oltre il dominio stesso di riferimento del teorema.
Provo a spiegare questa affermazione con la dimostrazione del teorema di uguaglianza degli angoli alla base di un triangolo isoscele. Diamo questa formulazione della tesi del nostro teorema:
«Dato un vertice A di un triangolo e due lati AB e AC che si congiungono in A, se AB=AC allora anche gli angoli ABC e ACB saranno uguali».
Dimostrazione per costruzione
Dato il triangolo in figura (disegnato in modo "neutro", cioè senza evidenziare nel disegno quanto si vuole dimostrare, vale a dire l'uguaglianza degli angoli alla base):
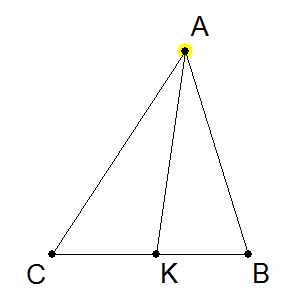
Tracciamo la bisettrice del vertice in A; questa retta incontra il lato BC nel punto K, come dalla figura seguente:
A questo punto, se guardiamo i triangoli ACK e AKB, sappiamo che:
- AC = AB in quanto per ipotesi i lati sono uguali (triangolo isoscele)
- AK è in comune
- L'angolo CAK è uguale all'angolo KAB (perché abbiamo costruito AK come bisettrice dell'angolo in A).
Ma allora i triangoli ACK e AKB sono equivalenti (perché hanno uguali rispettivamente due lati corrispondenti e l'angolo fra essi compreso). Ma allora, dato che sono uguali, anche gli angoli corrispondenti sono uguali. E quindi ABC e ACB sono uguali.
Dimostrazione per assurdo
Per dimostrare il teorema "per assurdo" partiamo dalla stessa figura di base e tracciamo ugualmente la bisettrice del vertice in A. Tuttavia, a questo punto, poniamo che gli angoli ACK e ABK siano diversi e cerchiamo di ottenere, da questa supposizione, una contraddizione nel nostro ragionamento.
Il metodo potrebbe ricalcare quanto svolto in precedenza, cioè considerare i triangoli ACK e AKB. Questi triangoli non possono essere uguali, dato che ACK e ABK sono diversi per ipotesi di assurdo. Da questa "conseguenza" posso derivare tre conseguenze che portano tutte a un "assurdo", in forza dello stesso teorema citato sopra:
«Condizione necessaria e sufficiente perché due triangoli siano uguali è che abbiano uguali due lati e l'angolo fra essi compreso»
- I triangoli non sono uguali, quindi non può essere che AB=AC, ma questo è assurdo perché contraddice le ipotesi iniziali;
- I triangoli non sono uguali, quindi non può essere che gli angoli CAK e KAB siano uguali ma questo è assurdo perché contraddice il fatto che AK sia la bisettrice per costruzione dell'angolo in A;
- I triangoli non sono uguali, quindi non può essere che AK sia uguale... a se stesso!
In tutti e tre i casi abbiamo invocato qualcosa di più «forte» che la geometria o i suoi assiomi; nel terzo caso abbiamo addirittura invocato un ulteriore assioma logico di uguaglianza di un elemento con se stesso. Tutto per dire: non posso affermare che la tesi non sia vera: altrimenti cadrei in contraddizione.
Secondo caso d'esempio
Ma la dimostrazione per costruzione, purtroppo, non è sempre possibile. Consideriamo ad esempio il teorema che afferma che i numeri primi sono infiniti. La dimostrazione per assurdo di questa tesi è piuttosto banale. Supponiamo infatti che i numeri primi siano in numero finito n. Consideriamo quindi il loro prodotto
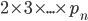
A questo numero aggiungiamo 1, ottenendo quindi:
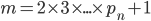
Ragioniamo sulla divisibilità di 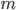 . Possiamo notare che, ad esempio, siccome il prodotto di tutti i numeri primi è pari (in quanto multiplo di 2), allora
. Possiamo notare che, ad esempio, siccome il prodotto di tutti i numeri primi è pari (in quanto multiplo di 2), allora 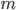 è dispari (perché ottenuto sommando 1 a questo prodotto). Cioè
è dispari (perché ottenuto sommando 1 a questo prodotto). Cioè 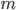 non è divisibile per 2. Analogamente
non è divisibile per 2. Analogamente 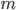 non può essere divisibile per 3, dato che il resto intero della divisione di
non può essere divisibile per 3, dato che il resto intero della divisione di 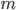 per 3 è proprio 1 (per costruzione di
per 3 è proprio 1 (per costruzione di 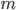 ). Ma questo si può affermare per ognuno degli
). Ma questo si può affermare per ognuno degli 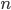 numeri primi, che abbiamo supposto in numero finito. Che cosa abbiamo ottenuto quindi? Abbiamo ottenuto un numero che non è divisibile per nessuno dei numeri primi. Ma allora abbiamo ottenuto un ulteriore numero primo; ma allora era assurdo supporre che i numeri primi fossero in numero finito; quindi i numeri primi sono infiniti.
numeri primi, che abbiamo supposto in numero finito. Che cosa abbiamo ottenuto quindi? Abbiamo ottenuto un numero che non è divisibile per nessuno dei numeri primi. Ma allora abbiamo ottenuto un ulteriore numero primo; ma allora era assurdo supporre che i numeri primi fossero in numero finito; quindi i numeri primi sono infiniti.
Viceversa: la regola che permetta di costruire "tutti" i numeri primi, se mai esistesse, non è comunque mai stata trovata. In assenza di questa "costruzione esibita", non rimane che procedere per assurdo, negando la tesi.
Cartesio e la geometria analitica
Tra l'altro la dimostrazione per costruzione, che costituisce un eccellente metodo di dimostrare checchessia, ha costituito però una delle spinte che hanno portato, fra gli altri, Cartesio, ad avvertire la necessità... di inventarsi una nuova geometria. Che cos'ha dunque la dimostrazione per costruzione di tanto brutto da aver spinto il "nostro" a cercare qualcos'altro? Il fatto è che è assolutamente imprevedibile. Il problema è duplice:
- Come si fa a sapere a priori quale teorema ammette una dimostrazione per costruzione?
- Inoltre, di tutti gli oggetti matematici che hanno un senso in relazione alla tesi che si vorrebbe dimostrare, qual è il «marchingegno» che porta alla dimostrazione della tesi?
La geometria euclidea è sintetica (descrive correttamente e approfonditamente gli oggetti del suo dominio; sull'esaurientemente, come si diceva nell'articolo precedente, ora non è più il caso di insistere...); ma non dà alcuna indicazione esplicita o implicita che possa indicare la strada per poter dimostrare nessun nuovo teorema. Le costruzioni sono una sorta di coup de théâtre imprevedibile.
E allora che fare? Ecco che Cartesio inizia a traslare il problema verso l'algebra (movimento che sarà completo e soprattutto pienamente consapevole solo con Hilbert e il programma di Erlangen). Descrivendo in termini di coordinate i problemi della geometria, non solo le soluzioni possono essere date per via algebrica ma, nel caso delle coniche, sono pure, all'indietro, costruibili con riga e compasso. Per certi versi l'algebra costituisce una sorta di centina verso costruzioni elementari altrimenti inimmaginabili.