Qualche giorno fa' mi sono imbattuto, pensando alla forma sferica dei cactus, nel problema isoperimetrico, cioè nella dimostrazione che, a parità di superficie, la figura geometrica piana con il perimetro minimo è la circonferenza. Un analogo vale per le dimensioni maggiori a 2.
Questo mi ha dato lo spunto per provare a invertire il problema: data una superficie finita, qual è la figura con perimetro massimo. E ho ottenuto abbastanza facilmente che il problema non ha soluzioni, nel senso che è possibile determinare una figura con superficie finita e perimetro infinito. Un figura che rappresenta quanto affermo sopra è l'oggetto del presente articolo.
Descrizione costruttiva della Seppia
La «Seppia», che chiamo così per a somiglianza con il mollusco, si ottiene a partire da una circonferenza di raggio r. In particolare consideriamo di tracciare una circonferenza concentrica e di raggio r/2. Questa circonferenza interna divide il cerchio originario in un cerchio interno di raggio r/2 appunto e in una corona circolare. Immaginiamo ora di dividere la corona circolare in tre parti uguali tracciando due raggi della circonferenza esterna, che formano un angolo di 120°.
Ciò che si ottiene somiglia all'immagine sotto:
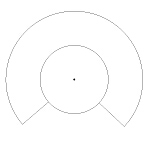
La nostra figura (la «Seppia», per intenderci) sarà costituita dall'arco di circonferenza corrispondente ai 
della circonferenza di raggio r, a cui aggiungiamo i due segmenti lunghi 
tracciati verso il centro delle circonferenze concentriche. In un primo momento la figura appare così:
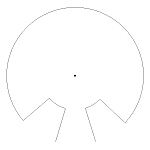
Immaginiamo a questo punto di iterare la divisione per tre dell'ulteriore spicchio rimanente. La nostra spezzata prosegue sulla circonferenza interna, lungo due archi che sottendono a loro volta angoli che sono un terzo del precedente; dalla fine degli archi si dipartono ulteriori "semiraggi" che raggiungono la circonferenza esterna. Il passo successivo ci avrà quindi permesso di tracciare la figura seguente:
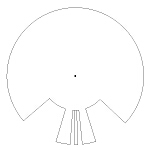
Ma da qui in avanti il procedimento è semplice: basta iterare la divisione per tre dell'angolo così ottenuto e tracciare i semiraggi alternativamente verso la circonferenza interna e verso quella esterna. Le ulteriori rappresentazioni della nostra figura saranno quindi:
seguita da:
e così via all'infinito. Tra l'altro la ragione per cui l'ho chiamata Seppia è che i segmenti in basso somigliano ai tentacoli e l'arco di di circonferenza, in alto, somiglia al mantello.
Dimostrazione che il perimetro è infinito
Questa dimostrazione è banale; siccome il perimetro è dato dalla somma di infiniti addendi di misura , è semplice constatare che questa somma è infinita. Allo stesso modo è facile mostrare che la superficie è invece finita; di fatto la seppia è completamente contenuta all'interno del cerchio di raggio r, quindi in particolare la sua superficie è strettamente inferiore alla superficie del cerchio. E quindi, in particolare, è finita.
Calcolo della superficie
Un poco più complesso è calcolare quanto misura la superficie della Seppia. Sicuramente possiamo affermare che la superficie della seppia è data dal cerchio di raggio sommata alla superficie della parte ottenuta a partire dalla corona circolare, iterando aggiunte e sottrazioni successive.
Quindi, ricordando che la superficie del cerchio è data da:
si ricava facilmente che la superficie del cerchio di raggio è 
da cui possiamo ricavare che la superficie della corona circolare sarà:
Se, a questo punto, consideriamo come abbiamo costruito la Seppia, vediamo che la sua superficie è data dal cerchio interno, a cui sommiamo la corona circolare, da cui però togliamo un terzo. Quindi aggiungiamo un terzo della parte rimossa, da cui togliamo un ulteriore terzo e così via, alternando aggiunte e sottrazioni sempre della terza parte rispetto alla precedente. Si arriva così alla formula seguente, per la superficie della Seppia:
Per procedere oltre con i nostri calcoli abbiamo a questo punto bisogno di tre lemmi.
Lemma 1 Somma della serie geometrica
Se consideriamo le somme parziali 
della serie geometrica, si dimostra per induzione che vale il risultato seguente:
e quindi, con un passaggio al limite, otteniamo (per q<1):
Lemma 2 (Teorema di Riemann)
«Una serie è incondizionatamente convergente se e solo se è assolutamente convergente»
Non darò la dimostrazione di questo teorema, che è possibile trovare in rete o su vari test di Analisi Matematica. Mi limiterò invece a spiegare... che cosa significa.
Una serie è assolutamente convergente quando converge la serie che ha, come termine generale, il valore assoluto del termine generale della serie di partenza. In formule, 
converge assolutamente se e solo se 
converge.
Una serie è incondizionatamente convergente quando la sua convergenza è indipendente da qualsiasi riordino dei suoi termini. Detto in altri termini: quando la somma infinita risultante gode della proprietà commutativa.
Quindi: per poter riordinare i termini della nostra serie, dovremo prima dimostrare che si tratta di una serie assolutamente convergente, il che è oggetto del Lemma successivo.
Lemma 3: La serie ottenuta dal calcolo della superficie della seppia, converge assolutamente.
Torniamo quindi a:
questo può essere interpretato come:
dove 
Se noi consideriamo la serie a termini alterni, la serie che otteniamo considerando il valore assoluto del termine generale, è la serie geometrica, che è una serie convergente. Quindi, in particolare, la nostra serie converge assolutamente, quindi converge incondizionatamente; cioè possiamo riordinarne gli addendi.
Alcuni calcoli finali
Con una permutazione (possibile per i lemmi 2 e 3) si possono ottenere i passaggi seguenti:
ma, per il Lemma 1, sappiamo che:
e quindi:
La «Seppia» ha quindi perimetro infinito e superficie 
.