Quali sono i limiti della conoscenza umana? La domanda si presta alle più svariate interpretazioni, prima ancora che alle più contrapposte "soluzioni". Esistono risposte filosofiche, così come religiose e morali; esiste persino la risposta di non voler investigare più a fondo come si fa in argomenti che, per il proprio sentire o per comune assenso della società, possano essere identificati come scabrosi. L'argomento è troppo vasto per essere affrontato, sia in termini di estensione (ricorsiva) del concetto, sia in termini delle mie limitate conoscenze (!). Quella che qui propongo è quindi solo una visione estremamente parziale e ristretta: limitiamoci a (una piccola parte di) ciò che possiamo affermare con certezza e che possiamo anche dimostrare; limitiamoci a un breve accenno elementare alla trattazione logico-matematica.
La principale fonte di questo post è una conferenza del MIT, soprattutto per quello che riguarda la traccia della dimostrazione che darò nel seguito.
2500 anni in poche righe
Che cosa è possibile conoscere? La prima risposta (filosofica, di quando la filosofia non era distinta né dalla scienza né dalla poesia) l'ha data Parmenide, con la celebre affermazione: "L'essere è, è conoscibile, è comunicabile con il pensiero razionale". Certo, col senno di poi potrebbe essere un tantino imprecisa; ma viene anche da pensare: "Provate a immaginare che cosa ne sarebbe stato della conoscenza umana se non avessimo, nei venticinque secoli seguenti, fatto affidamento su questa che non è una verità dimostrata ma piuttosto una speranza, se non avessimo creduto nella sua potenza di investigare il mondo?"
Le cose, dopo questo inizio programmatico, sono andate bene per secoli. A tratti anche benissimo, come quando da Galileo a Newton in avanti, il metodo scientifico sembrava aver confermato l'assunto e averlo portato a un compimento mai pensato prima. Addirittura all'inizio del 1900, con i lavori di Peano, Russell e Hilbert, sembrava fossimo a un passo dall'avere la teoria di dimostrazione di tutto. Non è stato che pochi anni dopo, nel 1931, che Gödel rovinò le uova nel paniere, dimostrando che, in ogni teoria matematica coerente (con altre condizioni tecniche che non serve qui approfondire) esiste almeno un predicato indecidibile.
Con questa dimostrazione svaniva il sogno che il logos potesse spingere la conoscenza ovunque; svaniva l'illusione che fosse solo questione di tempo il riuscirci. E invece no: c'erano luoghi in cui non si sarebbe mai potuti arrivare.
E da allora che cosa è successo? Occorre dir subito che due cose non sono successe: il teorema di incompletezza di Gödel non è rimasto chiuso in un cassetto ma ha permeato intere discipline logico-matematiche. Le conseguenze di questo teorema non hanno limitato lo sviluppo della matematica ma piuttosto le hanno dato un'impronta diversa, come un bastone messo in mano a una persona che si fosse improvvisamente accorta di camminare al buio; non le ha illuminato la strada ma le ha permesso di scansare pericoli fino ad allora ignorati.
Un semplice teorema
Negli ultimi anni un risvolto estremamente interessante di questo filone di pensiero è quello costituito dal seguente teorema, che mette insieme le nozioni dei numeri transfiniti di Cantor ed estende in qualche modo la portata della "incompletezza gödeliana". La tesi è la seguente:
La maggior parte dei problemi di decisione non sono computabili.
Prima di passare alla sua dimostrazione forse non è inutile notare che un "Problema di decisione" è una qualsiasi funzione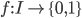 
dove 
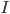può essere visto, genericamente, come l'insieme delle affermazioni esprimibili. Oppure, limitando la nostra attenzione a un suo sottinsieme "più interessante", consideriamo che 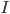sia l'insieme delle affermazioni formalmente corrette, coerenti e ben definite. Che cosa significa allora la funzione da 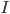ai valori 
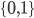? Banalmente significa: consideriamo la funzione che mappa queste affermazioni (o input, da cui la lettera 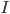normalmente utilizzata nella definizione) verso i due valori di verità 0 = FALSO e 1 = VERO.
In questi termini la tesi diventa:
Per la maggior parte delle affermazioni formalmente corrette, coerenti e ben definite, non è possibile ottenere una dimostrazione.
Lemma 1 - Gli algoritmi computazionali sono quanti i numeri naturali
Questa prima parte ci serve per calcolare quante sono le possibili "dimostrazioni" computazionali. La forma computazionale più banale è quella condotta da "umani". Dall'avvento dei calcolatori qualcuno si poteva essere illuso che, debitamente istruiti, i calcolatori potessero estendere indefinitamente la nostra capacità di trovare soluzioni e dimostrazioni. Questo teorema demolisce quelle illusioni.
Ogni procedimento dimostrativo può essere rappresentato come un algoritmo. Un algoritmo può essere descritto in modo intuitivo come un procedimento composto da un numero finito di passi, atto a risolvere un compito (che può essere eseguire un calcolo, ottenere una dimostrazione, risolvere un problema, ecc.). Esistono definizioni molto più rigorose ma, per lo scopo di questa breve chiacchierata, la descrizione intuitiva può essere sufficiente.
Addirittura possiamo anche considerare di sostituire il concetto di algoritmo con il concetto, ancora meno definito ma ancora più intuitivo, di "programma per calcolatore". Un programma è una sequenza di istruzioni (espresse in un linguaggio qualsiasi), composta da una successione finita di un numero finito di simboli, che possa venire interpretata ed eseguita dal calcolatore per svolgere il compito che descrive.
In questa seconda formulazione appare ancora più chiaro che ogni algoritmo
programma non è altro che una successione finita di "caratteri" presi da un insieme finito di caratteri possibili, e quindi rappresentabili secondo un "Dizionario". Altrettanto semplice è immaginare di rappresentare ognuno di questi caratteri attraverso un numero binario; e con pochi ulteriori accorgimenti di rappresentare ogni algoritmo in una stringa (finita per quanto lunga) binaria, quindi di 0 e 1.
Ogni algoritmo, quindi, è rappresentabile come una stringa binaria; ma ogni stringa binaria, di fatto, non è che un numero intero espresso in base 2. Si ha quindi:
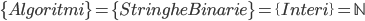
Lemma 2 - Le funzioni di decisione sono quante i numeri reali
Come accennato sopra i problemi di decisione sono dati dall'insieme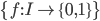 
. Quante sono queste funzioni? Chiaramente sono infinite come infiniti sono i numeri naturali. Ma sono "dello stesso ordine di infinito"? Ciò che si vuole dimostrare è che no, le funzioni di decisioni hanno la potenza del continuo, cioè hanno la cardinalità di 
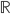, insieme dei numeri reali. Ora, siccome:
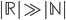
questo proverebbe la tesi iniziale (e spiegherebbe meglio che cosa si intende con "la maggior parte").
Ma questa dimostrazione è piuttosto semplice e utilizza lo stesso procedimento, detto metodo diagonale di Cantor, utilizzato già qui.
Dimostriamo allora il teorema. In effetti se le funzioni di decisione fossero quante i numeri naturali, questo significa che è anche possibile associare biunivocamente le funzioni ai numeri naturali. E quindi ordinare le funzioni associando la prima funzione al numero 1, la seconda al numero 2 e così via.
Consideriamo quindi la successione:
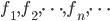
E ipotizziamo di costruire una nuova funzione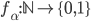 
in questo modo:
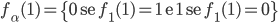
analogamente:
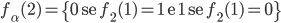
e così via.
Che cosa abbiamo ottenuto? Abbiamo costruito una funzione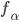 
che non coincide con 
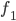, dato che almeno per il valore 1 le due funzioni differiscono. Ma non coincide nemmeno con 
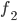, dato che almeno per il valore 2 le due funzioni differiscono. E' facile convincersi che 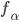non concide con nessuna delle funzioni della successione. Ma allora non è possibile ordinare le funzioni di decisione in una successione, dato che per ogni ordinamento che pone in relazione biunivoca le funzioni con 
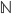è possibile costruire almeno una funzione che non sia compresa in questa successione. Ma allora queste funzioni sono di un infinito non numerabile. 