Narra una antica leggenda che la peste s'era diffusa ad Atene (o, secondo un'altra leggenda: a Delo) e che gli ateniesi non riuscissero a debellarla. Come sempre accadeva, quando le sole forze umane non bastavano e ci si riteneva di fronte a un portento, si ricorreva al responso degli dei. Per un ateniese il più qualificato dei responsi rimaneva quello dell'oracolo di Apollo a Delfi, dove la sacerdotessa, chiamata Pizia, rapita dai fumi del suolo e dell'alloro, avrebbe infine vaticinato.
E che cosa rispose l'oracolo? Rispose con un quesito matematico (manco a dirlo). Richiese di raddoppiare l'ara, di forma cubica, lasciandola inalterata quanto a dimensioni (cioè ottenere un nuovo cubo, che fosse il doppio del precedente).
Spesso, la prima volta che si incontra questo tipo di problema, ci si stupisce della difficoltà attribuita a questo tipo di richiesta. Perché dupicare un cubo non è oggettivamente difficile. A meno di non considerare le ulteriori condizioni al contorno che riguardano quali soluzioni erano da considerarsi accettabili per la mentalità di un antico greco e quali no.
In questo articolo cercherò di definire quali sono le esatte condizioni di accettabilità della soluzione.
Un salto a duemila anni dopo
Lasciatemi però, prima, riferire un ricordo di quando ero alla scuola media. Eravamo a metà degli anni 80 del secolo scorso. Un giorno la professoressa di Italiano, capitata non so più in che modo sull'argomento, ci chiese: "Ma come? Mi volete forse dire che non sapete qual è la definizione della retta?" Di fronte al nostro stupore, fu quasi sul punto di perdere le staffe. "Retta! Ho detto una retta, non una cosa così strana. Ma come fate a studiare la Geometria se non sapete nemmeno definirmi che cosa sia una retta?"
Ora devo ammettere che di quell'episodio non ricordo molto oltre il nostro stupore; non ricordo, ad esempio, come finì l'incidente diplomatico. Se non appunto così: con una sensazione di disagio che ancora a distanza di oltre trent'anni non ho ancora scordato.
Fatto sta che, con una soddisfazione ormai impropria e tardiva, ho poi imparato che la retta è proprio... indefinibile. Si tratta di un ente geometrico fondamentale, che viene dato senza descrizione. Per la semplice ragione che ogni descrizione di punto, retta o piano richiederebbe la descrizione di ulteriori elementi che li definiscano; e così via, ad infinitum. E che quindi, dagli Elementi di Euclide in avanti è parso un opportuno modo di procedere quello di non definire i concetti "intuitivi" di punto, retta o piano, appunto. Meno intuitivi sembrando altri concetti a cui forse si sarebbe tentati di ricorrere come "diritta", o "distanza", o "curva", o "breve" e così via.
In questo modo è lasciato al lettore di intendere che la retta sia il concetto astratto (l'archetipo, se così si vuol dire) di quella figura rappresentata, in natura, da un filo teso, dalla linea dell'orizzonte quando il mare è calmo, da un raggio di sole quando sbuca attraverso le nuvole.
Per gli antichi greci questo approccio, ben lungi dall'essere approssimativo, era perfettamente accettabile. Non solo: sulla base di un concetto come quello di retta e sul concetto di circonferenza, venivano ammessi tutta una serie di "costruzioni" (mentali) in un mondo ideale, non rappresentato se non imperfettamente da oggetti concreti, ma che potevano assurgere a vere e proprie dimostrazioni matematiche di teoremi, come è la consuetudine nella geometria Euclidea.
Costruzioni con riga e compasso
Ad esempio, consideriamo questa richiesta:
Dati due punti si trovi il loro punto medio (cioè il punto equidistante da entrambi).
Ecco come un antico greco non avrebbe ritenuto di poter procedere: non avrebbe "misurato" il segmento, dividendone la misura così ottenuta a metà e riportato questa "metà" sul segmento stesso. Non l'avrebbe fatto non perché sprovveduto, al contrario: perché non sarebbe stato così ingenuo dal non accorgersi della enorme approssimazione che comporta un'azione di questo tipo. Riflettiamo; stiamo parlando di:
- Verificare, rispetto a un'unità di misura esterna, a occhio, quanto un segmento sia lungo; cioè di avvicinare una scala graduata a un segmento e di "staccarne" la misura esatta.
- Stiamo considerando, ricavata questa misura, di procedere a dividerla a metà, approssimando eventualmente il risultato;
- E quindi nuovamente di avvicinare la scala graduata al nostro segmento, cercando di rilevare la graduazione più prossima alla misura calcolata. E da qui riportare, con una ulteriore approssimazione, il punto cercato sul nostro segmento iniziale.
Ma allora in che modo avremmo potuto pensare di procedere, salvaguardando la speranza ideale di ottenere non tanto la misura precisa in atto nel mondo reale, quanto di aver operato una serie di passi corretti nell'astrazione in cui possono essere concepiti? Il nostro antico greco avrebbe potuto procedere come segue.
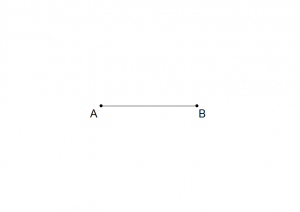
Immaginiamo di avere due punti, che chiamiamo A e B:
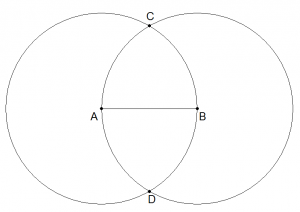
Tracciamo un segmento fra questi due punti. Quindi con un compasso puntato in A tracciamo una circonferenza di centro A e raggio AB. Analogamente tracciamo una circonferenza di centro B e raggio AB. Le due circonferenze si incontreranno in due punti C e D, come in figura:
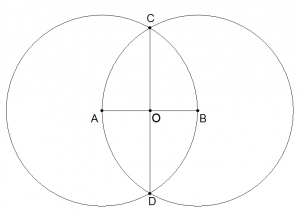
Se ora tracciamo un segmento fra C e D, questo interseca AB in un punto che chiamiamo O.
Il punto O è esattamente quanto cercato, cioè il punto medio fra A e B.
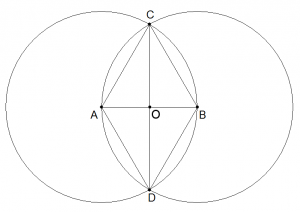
Dim: Consideriamo infatti il poligono formato da ADBC; per costruzione sappiamo che C e D si trovano sulla circonferenza con centro in A e raggio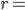 
AB da cui AC=AD. Allo stesso modo otteniamo che CB=BD ma anche AC=AD=CB=BD e cioè la figura è un parallelogrammo.
Dalle uguaglianze appena stabilite possiamo dedurre:
- Sono uguali gli angoli
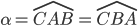in quanto angoli alla base di un triangolo isoscele; - Sono uguali gli angoli
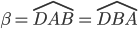in quanto angoli alla base di un triangolo isoscele; - Sono quindi uguali i triangoli CAD e CBD in quanto hanno uguali i lato AC con CB rispettivamente e AD con BD rispettivamente e hanno uguali gli angoli fra essi compresi (in quanto somma di angoli uguali
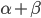). - Ma allora CD biseca ACB (in quanto gli angoli sono uguali per le uguaglianze appena stabilite). Da questa uguaglianza e dall'uguaglianza
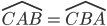si ottiene che anche i triangoli CAO e CBO sono uguali. - Ma allora saranno uguali i lati AO e OB, che era quanto si voleva determinare.
Ciò che occorre notare in questo procedimento sono, da un lato, il solo uso di una riga (cioè di uno strumento capace di tracciare segmenti di retta indefinitamente estesi) e di un compasso (cioè di uno strumento che possa tracciare una linea di punti equidistanti da un centro). Con queste unici strumenti mentali abbiamo potuto immaginare di tracciare segmenti ed archi e di intercettare i punti in cui questi si toccano, fino a ottenere una soluzione, per quanto ipotetica, del tutto esatta e rigorosa. Se i nostri strumenti fossero a precisione infinita, anche la soluzione rimarrebbe altrettanto corretta, senza subire alcun errore di arrotondamento.
Torniamo al nostro problema iniziale
Quando quindi i nostri scorati ateniesi ottennero il responso dell'oracolo, per ottenere quanto era stato loro richiesto non bastava quindi certo un calcolo approssimativo di quanto sarebbe dovuto essere il lato del nuovo cubo per ottenere che il volume fosse doppio. Ciò di cui avevano bisogno (spiritualmente bisogno, secondo la mentalità dell'antica grecia) era una costruzione, con riga e compasso, che permettesse loro di ottenere la costruzione mentale capace di realizzare in modo soddisfacente quanto la Pizia aveva imposto.
Purtroppo per loro una costruzione come questa è impossibile con riga e compasso. Nei prossimi articoli ci addentreremo nella dimostrazione (ottenuta solo con gli strumenti matematici messi a punto nel XIX secolo) dell'impossibilità di una tale dimostrazione.