Vediamo: è possibile scrivere un libro in cui esistano infiniti seguiti per ogni capitolo? Scopo di questo articolo è dimostrare che sì, disponendo di un tempo infinito, questo è possibile. Rimando all'articolo precedente la spiegazione del perché questa risposta non è ovvia e del perché la domanda non è banale (ad esempio, come mostrerò nell'articolo seguente: un libro così concepito non è possibile leggerlo, nemmeno disponendo di un tempo infinito).
La dimostrazione di questa affermazione consiste nel mostrare che esiste una corrispondenza biunivoca fra i numeri naturali e i capitoli del libro. In altri termini la dimostrazione si traduce in dover esibire una regola che permetta di determinare:
- quando ogni capitolo verrà scritto;
- che nessun capitolo possa essere omesso ma che tutti, in un tempo ben determinato, vengano scritti.
Nel primo caso sto descrivendo una funzione 
dove 
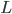è l'insieme costituito dai capitoli del libro; di più: devo mostrare che questa funzione è una biiezione (cioè è iniettiva e suriettiva).
Nel secondo caso devo mostrare che esiste 
e che anche questa è una biiezione.
Considerazione preliminare
Non sarebbe possibile immaginare di arrivare al successo ipotizzando una regola banale (oltre che, nel nostro caso, errata) come questa:
- Scrivo il primo capitolo;
- Scrivo i capitoli che sono il seguito del primo;
- Quando li avrò finiti, scriverò tutti i possibili seguiti ai seguiti, e così via.
Faccio notare due cose: che questa regola sarebbe applicabile se i seguiti di ogni capitolo fossero in numero finito; ma che, nel nostro caso, questa regola è inapplicabile: non arriverei mai a scrivere un capitolo che sia successione di uno dei seguiti del primo capitolo. Ad esempio: il seguito numero 5 del seguito numero 87 del primo capitolo, in questo modo, non so quando arriverò mai a scriverlo. Quindi questa regola va scartata perché non porta alla dimostrazione dell'assunto.
Ma allora? Appare evidente che occorrerà trovare un modo per scrivere parte i seguiti "di primi livello", parte quelli di secondo, di terzo e così via.
Una strada per uscire dal labirinto
Non dico che non esistano altre strade, ma la strada che ho immaginato di percorrere io si basa su due teoremi, alla base dell'aritmetica.
- Il primo teorema indica che i numeri primi sono infiniti.
- Il secondo (detto: "Teorema fondamentale dell'aritmetica") indica che ogni numero naturale maggiore di 1 può essere espresso come prodotto di un numero finito di numeri primi elevati a certe potenze. E che, fatto fondamentale, questa rappresentazione è unica.
Le dimostrazioni di entrambi i teoremi sono molto note e in rete se ne possono trovare ovunque; per cui a queste dimostrazioni rimando.
Vediamo invece come sfruttarli per fornire una modalità di costruzione della strada che ci permetta di scrivere questo libro.
Identifichiamo, senza troppa fantasia, il primo capitolo con il numero 1.
1
Passiamo ora a identificare i seguiti di questo capitolo. Assocerò al primo di questi seguiti il numero 2, al secondo il numero 3, al terzo il numero 5, al quarto il numero 7,... Come avrete immaginato: la regola è di associare ad ogni capitolo un numero primo. Ho abbastanza numeri per farlo? Sì, per il primo teorema che ho richiamato, i numeri primi sono infiniti quindi posso associare ad ogni seguito del primo capitolo un numero primo.
1
2 3 5 7
Vediamo ora i seguiti del primo seguito (ricordo che stiamo parlando del capitolo associato al numero 2, cioè al "primo" numero primo). Di nuovo posso utilizzare lo stesso sistema: ad ogni capitolo associo un numero primo partendo da 2.
Se però passo al secondo seguito (cioè il capitolo identificato dal numero 3), la regola cambia leggermente: assocerò sì ad ogni capitolo un numero primo, ma partendo dal numero 3 come primo numero che posso utilizzare.
La regola generale che applicherò sarà quindi che in ogni seguito n di ogni capitolo utilizzerò i numeri primi solo a partire dal numero primo "base" per quel capitolo. Questo mi garantisce circa il fatto che non potrò avere un capitolo associato a 2 seguito da un capitolo associato a 3 e di avere, al tempo stesso, un capitolo 3 associato a un successivo capitolo 2.
1
2 3 5
2 3 5 7 ... 3 5 7 11... 5 7 11 13 ...
In questo modo, l'ordine naturale dei numeri primi mi permette, insieme al teorema fondamentale dell'aritmetica, ricordato prima, di avere un unico modo di scrivere un capitolo.
Devo ora dimostrare che questa regola è biunivoca: lo dimostro in due passi. Mostro prima che ad ogni numero intero corrisponde un capitolo. Ma questo è semplice: per trovare a quale capitolo corrisponde il generico numero 
, occorre innanzitutto scomporre il numero nei suoi fattori primi con le relative potenze.
Mettiamo che sia 
per certi primi 
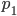e certi esponenti interi 
e mettiamo anche che i vari primi ,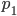 
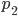, ecc. siano ordinati in modo crescente (<<...<
).
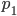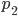Ma allora 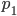è un capitolo di seguito (di primo livello) di 1; mi dice quante volte (eventualmente =1 mi dice: una sola volta) dopo aver preso la strada 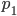devo prendere il primo seguito di tale capitolo. Con 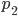le cose sono appena diverse, dato che i numeri primi che considero partono da 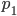e non più da 2, ma il discorso rimane uguale: prendo il 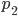-esimo seguito del capitolo individuato al passo precedente e così via.
Viceversa, diciamo che vogliamo trovare a quale numero corrisponde lo scrivere, ad esempio, il seguito numero 5 del seguito numero 87 del primo capitolo.
Innanzitutto il seguito numero 87 del primo capitolo è associato all'ottantasettesimo numero primo, che è 449. Da qui dovremo prendere il quinto seguito; ma il quinto, ricordo la regola, è il quarto (5 - 1) numero primo successivo all'ottantasettesimo, quindi il 467. Il numero intero associato a questo capitolo è dato quindi dal prodotto dei due, vale a dire 449 x 467 = 209.683.
Tornando indietro dal 209.683 vediamo che in effetti l'unica scomposizione di questo numero è proprio 449 x 467 (dato che sono entrambi primi). Quindi: ordino 449 e 467 in modo crescente. Prendo il primo: 449. Ma questo è l'ottantasettesimo numero primo. Quindi ricostruisco che devo scrivere:
- capitolo iniziale (1)
- capitolo successivo numero 87 (449);
- capitolo successivo numero 5 (87+5-1=91; quindi novantunesimo numero primo: 467)
In questo modo ad ogni numero corrisponde un capitolo e viceversa. Quindi ogni capitolo del libro posso predire quando verrà scritto e non ci sono numeri che non hanno una scomposizione in fattori primi, quindi nessun capitolo verrà omesso.
Ma allora i capitoli di questo libro sono esattamente tanti quanti i numeri naturali, quindi sono esattamente tanti quanti i capitoli di un libro in cui, ad ogni capitolo, ne segua esattamente uno.
Del resto, come si diceva: il bello viene nel prossimo articolo.