Nei due articoli precedenti (Se un giorno un alieno ci parlasse... e ...noi che cosa capiremmo?) illustravo la difficoltà di comunicazione con un ipotetico interlocutore alieno in assenza di una preventiva condivisione di un canale e di un metodo. Mi concentravo quindi sulla possibilità di trasmettere entità numeriche come dato assoluto da condividere, a vantaggio di altre informazioni inestricabilmente dipendenti da dati locali come l'impronta biologica o la storia evolutiva (o storia tout-court) del genere umano.
Dando per acquisito che sia possibile, anche se non immediato, trasferire numeri in modo intelligibile in questo articolo vorrei trattare un ulteriore argomento che può essere espresso come:
"Quali numeri potremmo utilizzare per comunicare a una intelligenza aliena la nostra conoscenza dell'universo?"
Quali numeri non riusciremmo a inviare
Ci sono entità fisiche che, per loro natura, supponiamo debbano essere costanti in tutto l'universo. Ad esempio: la forza con cui si attraggono i corpi (siano essi pianeti, galassie o mele) abbiamo scoperto da secoli essere proporzionale alle loro masse, all'inverso del quadrato delle distanze e a un valore costante. Sarebbe bello poter inviare questo numero costante da una parte all'altra dell'universo, per poter dire: "Ehi, anche noi questa cosa l'abbiamo capita!" Tuttavia, spiace dirlo, questa comunicazione non è possibile.
La perentorietà dell'affermazione precedente deriva dal fatto che questo stesso numero può essere rappresentato in infiniti modi diversi, in funzione del sistema di misura che si adotta. Se invece del metro (convenzionale unità di misura delle lunghezze, derivante dalla comodità di misurazione rapportata alle proporzioni umane) e del secondo (convenzionale unità di misura del tempo, derivante dalla durata della rotazione terrestre, scomposta in sottomultipli), venissero scelte altre unità di misura, il valore che conosciamo per la costante G sarebbe completamente differente.
E lo stesso può essere detto per ogni altra misurazione dell'universo che, per quanto possa avere valore universale, per essere espressa ha bisogno di un sistema di riferimento, quindi di una convenzione accettata fra i soggetti della comunicazione.
In particolare, giusto a titolo di esempio, vediamo quanto il metro sia convenzionale. Di fatto si tratta di una misura "grossomodo paragonabile" alle dimensioni umane. Può essere simile a un passo umano, arcaico strumento di misurazione delle distanze da percorrere a piedi e da questo derivare. Per poter essere "astratto e generalizzato", in tempi di Rivoluzione Francese, nel 1791, venne stabilito di considerare metro quella che era ritenuta, per le stime dell'epoca, la decimilionesima parte della distanza fra il Polo e L'Equatore terrestre. Elaborazioni e accordi internazionali successivi non hanno fatto che perfezionare sia la misura, sia la modalità di ottenerla, senza mai alterare la natura puramente convenzionale del concetto di metro.
Come conseguenza della convenzionalità del metro, sia ha, ad esempio, la convenzionalità della misurazione del volume (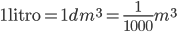 ). E quindi della massa, dato che un Kg è la massa di acqua distillata a temperatura e pressione fisse e stabilite che occupa il volume di un litro. Se la nostra nozione di massa, per essere misurata, si basa su una convenzione, è facile convincersi quanto tutte le costanti che hanno attinenza con la gravitazione siano a loro volta espresse per mezzo di convenzioni.
). E quindi della massa, dato che un Kg è la massa di acqua distillata a temperatura e pressione fisse e stabilite che occupa il volume di un litro. Se la nostra nozione di massa, per essere misurata, si basa su una convenzione, è facile convincersi quanto tutte le costanti che hanno attinenza con la gravitazione siano a loro volta espresse per mezzo di convenzioni.
I numeri adimensionali
Ciò che ci servirebbe è quindi, dopo tutti i ragionamenti fatti, un numero con queste caratteristiche:
- Deve essere adimensionale, cioè non dipendente dalla scelta di uno specifico sistema di riferimento;
- Deve veicolare informazioni che esprimano una attestazione della nostra conoscenza dell'universo.
Chiaramente la prima condizione è necessaria, perché si possa instaurare la comunicazione. La seconda è una mia idea, in linea con quanto ho scritto in questi tre articoli, ma evidentemente del tutto opinabile.
Fra i numeri che rispettano la condizione 1 ci sono numeri molto noti fra cui:
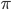 - "Pi greco" cioè il rapporto fra il raggio e la circonferenza di un cerchio;
- "Pi greco" cioè il rapporto fra il raggio e la circonferenza di un cerchio; - "Numero di Nepero" cioè la base della funzione esponenziale;
- "Numero di Nepero" cioè la base della funzione esponenziale;- ecc.
Questi numeri esprimono conoscenze matematiche che possono non implicare una profonda conoscenza del mondo fisico. Tra l'altro si tratta di numeri trovati anticamente dall'umanità, prima ancora di avere un'idea di che cosa fosse la scala dell'universo a cui siamo soliti pensare oggi. Addirittura Pi greco era stato approssimato dagli egiziani come 3, compiendo sì un errore di arrotondamento significativo, ma esprimendo, al tempo stesso, un concetto piuttosto rilevante come: "Il valore costante del rapporto fra un raggio e la circonferenza, per ogni cerchio al mondo, è pari a...".
Il mio personale candidato come veicolo di informazioni, a livello della chiacchierata che sto portando avanti in questi tre articoli, è un altro numero, un numero che esprime un concetto più strettamente correlato con la fisica, pur essendo un numero adimensionale. In particolare si tratta della prima costante di Feigenbaum. Nel prossimo paragrafo descriverò di che cosa si tratta.
Il numero di Feigenbaum
Il primo numero di Feigenbaum (le costanti di Feigenbaum in realtà sono due, ma qui la mia scelta cade semplicemente sulla prima), è un numero che esprime un concetto fisico molto chiaro:
"Dato un qualsiasi fenomeno fisico, di qualsiasi natura, il primo numero di Feigenbaum permette di predire quando il caos irromperà nel sistema."
L'affermazione sopra suona come molto impegnativa. Qualsiasi fenomeno fisico è un concetto veramente esteso; qualsiasi fenomeno a noi del tutto sconosciuto, ma magari noto alla nostra controparte aliena dell'ipotetica comunicazione, deve essere soggetto a questo tipo di comportamento. Ce n'è, a mio modo di vedere, di che ritenere la spiegazione che segue, quantomeno interessante.
Vediamo innanzitutto come ottenere il primo numero di Feigenbaum. In un successivo articolo, mostrerò come usare OpenOffice calc per effettuare questo tipo di "analisi euristica" non certo tecnicamente insindacabile ma efficace e suggestiva.
Consideriamo, per definizione, una qualsiasi funzione reale, definita positiva, tre volte derivabile su [0;1] e dotata di un unico massimo su questo intervallo. Il concetto di "qualsiasi funzione", come si vede, lascia uno spazio notevole alla fantasia umana o aliena che sia... Vediamo alcuni esempi di queste funzioni:
- "Mappa logistica" - La prima funzione studiata in questo senso. Può essere espressa come:
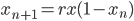 ;
; 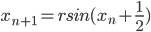 ;
;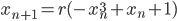 ;
;- ...
e così via per ognuna delle infinite possibilità di funzioni reali che rispettino le caratteristiche indicate sopra. Che cosa accumuna tutte queste funzioni? Insospettabilmente hanno una caratteristica in comune, relativa al coefficiente 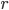 visto come variabile di una ulteriore funzione.
visto come variabile di una ulteriore funzione.
In particolare, partendo dalla prima funzione elencata, possiamo definire:
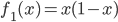 e
e 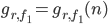 dove
dove  è l'indice della nostra successione.
è l'indice della nostra successione.
Allo stesso modo potremmo indicare: 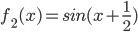 e
e 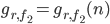 ecc.
ecc.
Che cosa succede se consideriamo ora
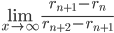 ?
?
E qui la scoperta è stata entusiasmante (i gusti son gusti, ovviamente!). Tutte queste funzioni hanno un comportamento simile che può essere illustrato dall'analisi della Mappa Logistica. In particolare il limite a cui tende la funzione è unico per 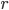 sotto a un certo valore soglia. Da un certo valore in avanti il limite si "sdoppia" nel senso che non esisterà più un solo valore limite ma i valori diventeranno due, via via divergenti al crescere ulteriore di
sotto a un certo valore soglia. Da un certo valore in avanti il limite si "sdoppia" nel senso che non esisterà più un solo valore limite ma i valori diventeranno due, via via divergenti al crescere ulteriore di 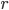 . E la stranezza non finisce qui, perché continuando a far crescere
. E la stranezza non finisce qui, perché continuando a far crescere 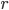 , ognuno dei due rami si biforca ulteriormente, facendo passare i valori limite a 4, 16 e così via. Che cosa rappresenta quindi la prima costante di Feigenbaum? Rappresenta il valore (costante per ogni funzione immaginabile!) del rapporto fra due valori successivi di
, ognuno dei due rami si biforca ulteriormente, facendo passare i valori limite a 4, 16 e così via. Che cosa rappresenta quindi la prima costante di Feigenbaum? Rappresenta il valore (costante per ogni funzione immaginabile!) del rapporto fra due valori successivi di 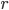 per cui assistiamo a una biforcazione.
per cui assistiamo a una biforcazione.
Questo numero, in particolare, si approssima come δ = 4,66920160910299067185320382
Conclusioni
Che cosa succederebbe quindi se inviassimo un unico messaggio con una rappresentazione di 4,66920160910299067185320382 verso un'entità aliena?
La risposta più divertente che ho immaginato è che gli alieni ci possano rispondere con un numero come:
57,234231456346234523458245324527
Numero di cui cui, a oggi, non sappiamo ancora nulla.
