L'impossibile soluzione

Messe insieme alcune informazioni necessarie, eccoci a trovare la soluzione del problema che aveva angustiato i nostri poveri ateniesi. In effetti non è rimasto molto da provare; al più occorre riprendere il filo logico del discorso.

Lemma

L'equazione 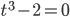è irriducibile in .

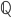Dim: La dimostrazione è per assurdo. Ipotizziamo che sia 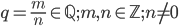e con la frazione già ridotta ai minimi termini. Supponiamo che 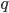sia una radice di .

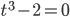Ricordiamo per il teorema di unicità di scomposizione in fattori primi abbiamo che:

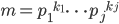
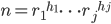
per 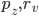primi. Dato che abbiamo supposto che 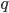sia una radice del polinomio di partenza, otteniamo di poter riscrivere l'equazione come

.

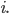
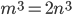Possiamo considerare due casi:

• se 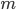è divisibile per 2, nella scomposizione in fattori primi di 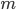, uno dei 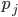deve essere il primo 2. Ma allora 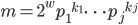per un 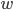intero positivo. Siccome abbiamo supposto ch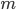e e siano già ridotti, otteniamo che non deve essere divisibile per 2. Ricordando l'equazione 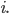si ottiene che 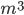sarà divisibile per 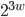mentre l'elemento a destra dell'equazione sarà divisibile solo per 2. Quindi è assurdo supporre che 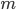sia divisibile per 2.
• se 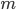non è divisibile per due, allora la 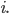implica che a sinistra non ci sia, fra i fattori, il numero primo 2 mentre a destra c'è, con esponente maggiore o uguale a 1. Il che è nuovamente assurdo.

Quindi non esistono soluzioni di 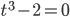in .

Ripartiamo quindi dalle considerazioni svolte nell'articolo precedente.

I nostri due punti di partenza sono 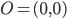e 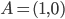e il segmento 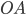è il lato del nostro cubo di partenza. Sappiamo allora che tutti i punti che possiamo costruire tramite riga e compasso a partire dai 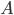e 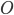sono soluzioni di equazioni di primo o di secondo grado. A loro volta i punti che possono essere costruiti, a partire dai punti così generati, saranno ancora soluzioni di equazioni di primo o di secondo grado. Quindi l'ennesimo punto ottenuto, con riga e compasso, a partire dai due punti base, sarà soluzione di un'equazione di grado 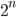per un qualche intero .

E questo basta per concludere che il punto 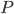di coordinate 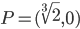, non essendo radice di una soluzione di grado pari (per l'irriducibilità mostrata sopra), non potrà mai essere costruito con riga e compasso.