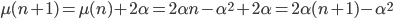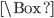L'occasione di riscrivermi daccapo una tavola pitagorica me l'ha data mio figlio Marco che, in seconda elementare, s'è trovato a dover studiare le tabelline. Ed ecco che dopo aver scritto, in bella grafia, tutti e 100 i numeri, butto lì una domanda:
"Ma, secondo te, in questo quadrato da 100 numeri, sono più i numeri pari o quelli dispari?"
Dai semplici e futili ragionamenti che sono seguiti si origina questo articolo.
Contare i pari
Per contare i numeri pari si può fare un semplice ragionamento di questo tipo:
- Sono pari tutti i numeri contenuti sulle righe pari, cioè la seconda, la quarta, ecc.
- Sono pari anche, sulle righe dispari, un numero su due (in particolare: quelli sulle colonne pari).
Da qui si deduce molto semplicemente che il numero dei pari è dato da:
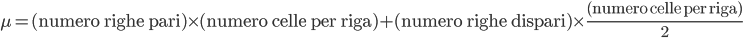
ma quindi:
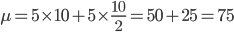
Quindi, nonostante a priori, fidandosi avventatamente della "simmetria" della tavola pitagorica, si potrebbe immaginare che questa si trascini anche sul conteggio di pari verso dispari, ecco che i pari sono ben i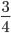 
dei numeri, relegando i dispari ad appena 
.
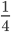Una semplice immagine rende bene evidente questa "dominanza" dei pari:
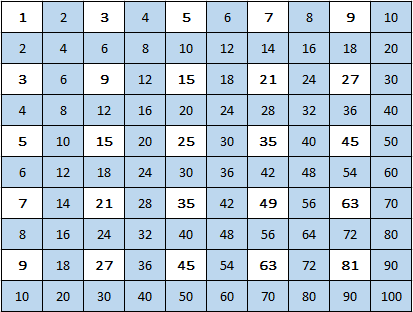
Ma a questo punto la curiosità si potrebbe espandere fino a includere quadrati di lato maggiore e numeri diversi da 2. Sul primo elemento (lato del quadrato) non ci sono apparenti restrizioni, nell'ottica di mantenere il discorso sufficientemente semplice. Nel secondo caso abbiamo invece bisogno, almeno inizialmente, di limitare la nostra attenzione ai soli numeri primi.
Ragioniamo infatti su una delle assunzioni che ci conviene fare nel passare da 2 a "un numero maggiore". Con il 2 i calcoli venivano bene (erano addirittura banali) perché il fatto che 2 sia un numero primo ci poneva nella gradevole condizione che i suoi multipli dovessero trovarsi esclusivamente nelle righe o nelle colonne di posizione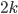 
per qualche intero 
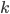. Questa condizione non viene invece garantita quando i numeri non sono primi; il più banale controesempio è dato dal più piccolo numero non primo, cioè 4, che mostra già come i multipli di 4 sono sì quelli che si trovano sulle righe e sulle colonne multiple di 4... ma anche altrove.
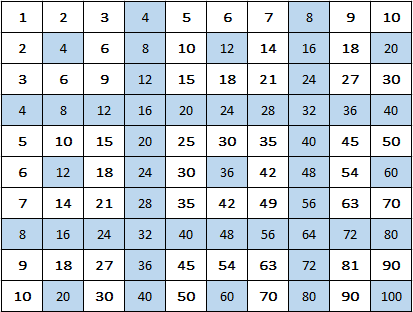
Lascerò la trattazione di questi numeri non primi a un articolo successivo. Veniamo ora invece alla prima generalizzazione del calcolo precedente.
I numeri multipli di un primo 
in un quadrato moltiplicativo 
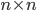
Per calcolare quanti sono i multipli di un intero primo in un quadrato moltiplicativo 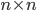basterà ripetere il ragionamento già fatto per il numero 2, con l'accortezza che se prima i numeri dispari erano la metà dei pari, ora occorre ragionare in classi di resti. Ad esempio, se consideriamo il numero 3, abbiamo queste tre classi:
- multipli di 3;
- multipli di 3 a cui aggiungiamo 1;
- multipli di 3 a cui aggiungiamo 2;
Ogni numero naturale appartiene a una e una sola di queste tre classi. Ricordo che con il numero due vale lo stesso discorso, che suona però nel modo (più familiare): "O un numero intero è pari o è dispari".
Rappresentiamo il tutto in termini matematici, ricordando che, per una conseguenza del Teorema fondamentale dell'aritmetica si ha che:
- dato un intero
(nel nostro caso numero di elementi su ogni riga e su ogni colonna della tavola moltiplicativa) - dato un numero primo con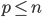
allora:
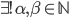tali che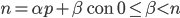 
in particolare chiamiamo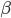 
il resto intero della divisione di per .
Graficamente possiamo pensare a questi numeri in modo abbastanza immediato, immaginandoci la figura seguente:
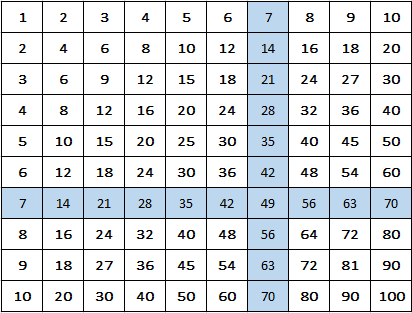
L'assenza di celle azzurre al di fuori delle righe e delle colonne interamente azzurre è data dalla definzione di numeri primi. Infatti: in azzurro abbiamo la riga che si trova in posizione ; tutte le precedenti corrispondono a numeri minori di . Sappiamo inoltre:
- tutte le celle sulla riga contengono esclusivamente numeri multipli di ;
- le celle sulle righe diverse da e dai suoi multipli contengono numeri multipli di soltanto se si trovano su colonne che corrispondono a multipli di
Ma a questo punto basterà calcolare tre valori per risolvere (in modo analogo a quanto avevamo fatto prima con il numero primo 2) il nostro problema. I quesiti sono:
- quante sono le righe (rispettivamente: colonne) che corrispondono a multipli di in un quadrato moltiplicativo ?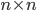
- quante, di conseguenza, le righe (colonne) non multiple di ?
- su queste righe (colonne) non multiple di , quanti sono i numeri multipli di ?
Per ottenere le risposte basta ricordare la formula: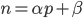 
Infatti:
- le righe che corrispondono a multipli sono esattamente
- le righe non multiple sono
- su queste righe le celle multiple sono tante quante le righe multiple, quindi di nuovo
questo porta a:
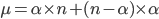
cioè:
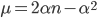
Osservazione: Applichiamo la formula al caso di partenza. Abbiamo: 
e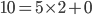 
, quindi 
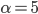e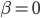 
da cui:
.
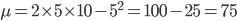L'ipotesi sembra allettante. Proviamo ora a dimostrarla.
Dimostrazione della formula generale (per induzione)
Occorre innanzitutto notare che si possono avere due casi, dando un'occhiata alla fig. 3. Possiamo avere, relativamente al nostro intero che, ricordo, è il lato del quadrato e al nostro primo , che è il primo di cui stiamo contanto i multipli una delle due relazioni:
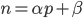con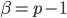 
oppure
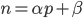con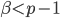 
Nel primo caso questo significa che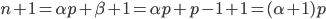 
Graficamente occorre immaginare che la situazione sia quella di un quadrato in cui aggiungendo una riga (e una colonna!) si ottenga che l'ulteriore aggiunta sia proprio una riga (colonna) azzurra, cioè una riga (colonna) di multipli.
Nel secondo caso la situazione è più semplice, dato che aggiungendo una riga (colonna) si ottiene una ulteriore riga (colonna) identica alla precedente, dato che con questa aggiunta, a causa della disuguaglianza stretta, non abbiamo raggiunto una riga di tutti multipli.
Caso 1: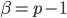
Supponendo che valga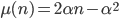 
, vediamo come diventa la tesi induttiva. In effetti occorre ricordare che 
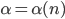e che non basta sostituire nella formula, ma anche stessa. Devo quindi provare che vale: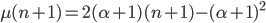 
e cioè, dopo alcuni calcoli, la mia tesi diventa:
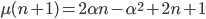
Ma dimostrare questo è semplice osservando che il quadrato di lato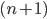 
è dato da un quadrato 
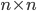con l'aggiunta di una riga e di una colonna (che hanno in comune una cella, da non contare quindi due volte) e che comportano l'aggiunta al quadrato di uno "gnomone" di 
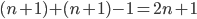celle. Non solo: queste celle aggiunte, per la definizione del caso 1, sono tutte multiple di o azzurre che dir si voglia. Quindi:
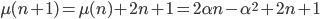che è proprio la nostra tesi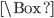 
Caso 2: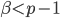
Il secondo caso è ancora più semplice, considerando il fatto che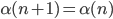 
. Infatti incrementando di una unità, non si ottiene il multiplo successivo di , cioè non si raggiunge l'ulteriore riga (colonna) azzurra.
La tesi induttiva sarà quindi, semplicemente:
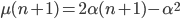
Come otteniamo geometricamente l'aggiunta di celle al nostro quadrato 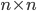? Semplice: aggiungeremo una riga (colonna) identica alla precedente. Quindi una riga (colonna) in cui i multipli di saranno esattamente , da cui l'aggiunta di 
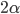celle multiple di . Ma allora:
