In un articolo precedente avevo trattato il caso semplice di calcolare, dato un primo  e un quadrato moltiplicativo (cioè un quadrato in cui il contenuto delle celle è dato dalla moltiplicazione del numero progressivo di riga per il numero progressivo di colonna), di dimensioni
e un quadrato moltiplicativo (cioè un quadrato in cui il contenuto delle celle è dato dalla moltiplicazione del numero progressivo di riga per il numero progressivo di colonna), di dimensioni 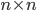 , quanti sono i multipli di
, quanti sono i multipli di  all'interno del quadrato. La semplificazione era rappresentata dal fatto di scegliere
all'interno del quadrato. La semplificazione era rappresentata dal fatto di scegliere  primo. Il risultato ottenuto era che, dati
primo. Il risultato ottenuto era che, dati  e
e 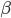 tali per cui
tali per cui 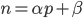 con
con 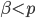 , allora la formula generale per il quadrato
, allora la formula generale per il quadrato 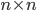 era
era 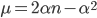 . Cerchiamo ora di fare un piccolo passo avanti: al posto di un primo
. Cerchiamo ora di fare un piccolo passo avanti: al posto di un primo  consideriamo un intero
consideriamo un intero 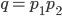 con
con 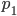 e
e 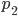 primi. Non siamo ancora all'
primi. Non siamo ancora all'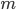 generico, ma ci stiamo avvicinando.
generico, ma ci stiamo avvicinando.
Differenziamo due ovvie casistiche: 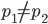 oppure
oppure 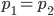 che condurranno a risultati differenti.
che condurranno a risultati differenti.
Multipli di 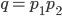 con
con 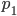 e
e 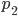 primi e
primi e 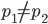
Espandiamo i ragionamenti svolti per  primo. Possiamo considerare che
primo. Possiamo considerare che 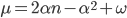 . E questo poiché
. E questo poiché 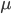 era costituito, per
era costituito, per  primo, da multipli che si trovavano esclusivamente su righe e colonne multiple di
primo, da multipli che si trovavano esclusivamente su righe e colonne multiple di  . A questi elementi andranno ora aggiunti altri elementi, derivanti dalla scomposizione in fattori. Quindi, nel caso generale, possiamo già affermare:
. A questi elementi andranno ora aggiunti altri elementi, derivanti dalla scomposizione in fattori. Quindi, nel caso generale, possiamo già affermare:
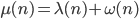 con:
con: 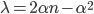 ; è inoltre facile convincersi che
; è inoltre facile convincersi che 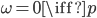 è primo. Osserviamo infatti che i multipli di
è primo. Osserviamo infatti che i multipli di 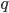 sono nelle celle che si trovano in una di queste condizioni:
sono nelle celle che si trovano in una di queste condizioni:
- si trovano su una riga o una colonna corrispondente a
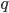 o a un suo multiplo (e questo dà, alla nostra formula, l'apporto
o a un suo multiplo (e questo dà, alla nostra formula, l'apporto 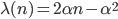 );
); - si trovano fuori da queste righe (rispettivamente: colonne) e, contati, contribuiscono per l'addendo
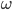 ;
;
Ma allora la considerazione che può condurci al conteggio di 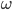 è che queste celle sono date da:
è che queste celle sono date da:
- righe multiple di
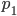 ma non multiple di
ma non multiple di 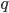 (dato che le multiple di
(dato che le multiple di 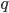 sono già contate dalla prima parte della formula);
sono già contate dalla prima parte della formula); - in queste righe gli elementi interessanti sono quelli che si trovano su colonne di posto di ordine
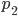 salvo, di nuovo, quelli multipli di
salvo, di nuovo, quelli multipli di 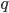 ;
; - un uguale apporto sarà quello in cui si invertono
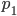 con
con 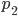 e in cui scambieremo righe con colonne.
e in cui scambieremo righe con colonne.
Quindi stiamo ipotizzando:
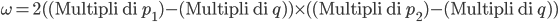
Ricordando che 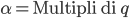 e definendo
e definendo 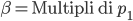 e
e 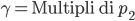 la nostra formula diventa:
la nostra formula diventa:
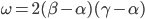
da cui la formula generale proposta (per il caso 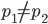 ) diventa:
) diventa:
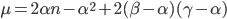 .
.
Prima di provare a dimostrarla, verifichiamola in un caso semplice; contrariamente a quanto si potrebbe essere portati a immaginare, è più semplice contare i multipli di 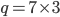 o di
o di 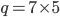 piuttosto che con primi più piccoli, come ad esempio il
piuttosto che con primi più piccoli, come ad esempio il 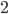 .
.
Infatti, quanti sono nella tavola pitagorica 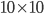 i multipli di 21? I numeri multipli di 21, inferiori a 100, sono soltanto 21, 42, 63 e 84. Tuttavia 84 non è presente nella nostra tavola dato che
i multipli di 21? I numeri multipli di 21, inferiori a 100, sono soltanto 21, 42, 63 e 84. Tuttavia 84 non è presente nella nostra tavola dato che 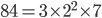 e in qualunque modo si combinino i fattori, si ottengono comunque scomposizioni in cui almeno un fattore è maggiore di 10. Quindi fattori che non hanno un numero di riga o di colonna compreso entro il 10, che è la condizione necessaria perché possano essere presenti nella tavola pitagorica.
e in qualunque modo si combinino i fattori, si ottengono comunque scomposizioni in cui almeno un fattore è maggiore di 10. Quindi fattori che non hanno un numero di riga o di colonna compreso entro il 10, che è la condizione necessaria perché possano essere presenti nella tavola pitagorica.
Rimangono 21, 42 e 63; ci si convince facilmente che tutti e tre questi numeri godono delle caratteristiche:
- non sono quadrati perfetti e quindi non si trovano sulla diagonale;
- questo fatto, unito alla commutatività della moltiplicazione, ci dice che dovremo trovare per ognuno di questi numeri almeno una coppia di celle che li contengono (invertendo la "coordinate");
- altre considerazioni di scomposizione in fattori, simili a quelle sul numero 84, ci assicurano che non ci sono altre possibilità di ottenere, con interi inferiori o uguali a 10, altre combinazioni che diano 21, 42 o 63 come risultato.
Da tutto questo otteniamo che tre numeri, ognuno in due possibili celle, portano a 6 possibili celle di multipli. (Certo: anche contarli direttamente ci avrebbe permesso di ottenere lo stesso conteggio...).
Verifichiamo la coerenza con la formula proposta:
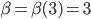
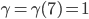
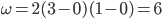
Multipli di 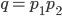 con
con 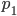 e
e 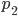 primi e
primi e 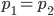 (cioè
(cioè 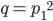 )
)
Osserviamo la tabella che evidenzia i multipli di 4.

Possiamo vedere che i multipli di 4 sono:
- sulle righe multiple di 4; in questo caso saranno tutte le celle delle righe;
- sulle righe multiple di 2; ma in questo caso occorre considerare due ulteriori informazioni:
- i multipli di 4 collideranno, nella metà esatta dei casi, con elementi che già di per sé, si trovano sulle righe azzurre e quindi sono già stati "contati" nella casistica precedente;
- rimangono quindi da contare gli elementi su righe multiple di 2, quando incrociano le colonne multiple di 2, ma considerando solo la metà di questa casistisca per l'osservazione precedente.
In questo caso la formula proposta diventa:
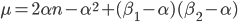 ma, dato che
ma, dato che 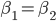 , si ha che:
, si ha che:
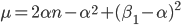
Verifichiamolo nel caso di 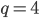 . In questo caso la parte
. In questo caso la parte 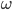 è quella che "conta" i quadratini azzurri isolati, cioè non contenuti in righe e/o colonne. Questi quadratini sono 9 (da conteggio diretto in figura!).
è quella che "conta" i quadratini azzurri isolati, cioè non contenuti in righe e/o colonne. Questi quadratini sono 9 (da conteggio diretto in figura!).
Verifichiamo l'accordo con la formula (relativamente alla parte 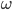 ):
):
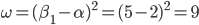 .
.
Analisi delle possibili casistiche
Come nel caso semplice dell'articolo precedente, occorre considerare che la situazione è differente in funzione di un certo numero di possibilità, tutte connesse all'aggiunta di una riga e di una colonna (dato che, nella dimostrazione per induzione su  , l'aggiunta di una unità a
, l'aggiunta di una unità a  corrisponde appunto ad aggiungere una riga e una colonna).
corrisponde appunto ad aggiungere una riga e una colonna).
Partendo dalla prima possibilità analizziamo: 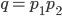 e
e 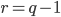 .
.
Questo significa che stiamo aggiungendo la riga "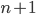 " che sarà di multipli di
" che sarà di multipli di 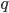 (e quindi anche di
(e quindi anche di 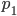 e di
e di 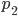 ). E questi multipli saranno in numero di
). E questi multipli saranno in numero di 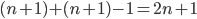 .
.
Due immagini ci possono aiutare per comprendere le altre casistiche. Ad esempio, consideriamo: 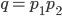 e
e 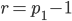 .
.

Nella nostra riga, fatta tutta da multipli di 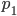 , saranno multipli di
, saranno multipli di 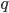 tutti i numeri che si trovano in celle su colonne multiple di
tutti i numeri che si trovano in celle su colonne multiple di 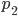 ; ma queste sono in numero di
; ma queste sono in numero di 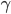 per definizione di
per definizione di 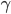 ; considerando l'apporto della riga e della colonna aggiunta, si ottiene quindi che l'apporto atteso è
; considerando l'apporto della riga e della colonna aggiunta, si ottiene quindi che l'apporto atteso è 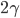 .
.
Analoghe considerazioni si possono fare considerando il caso di primi coincidenti, illustrato nella figura seguente:

Al termine di analoghi ragionamenti, la versione completa dei 7 casi possibili è quella rappresentata in tabella:
| Lingua isolata | Orologio Molecolare |
|---|---|
| Le variazioni casuali di lieve entità non influiscono sulla comprensione dei parlanti e quindi sull'efficacia (fitness) della lingua | Le variazioni sinonimiche dei Codoni non influiscono sulla fitness dell'individuo |
| La lingua evolve se nascono esigenze di utilizzare parole o concetti nuovi, dati da eventi differenti da quelli descritti dalla lingua | Il codice genetico è spinto a cambiare se cambiano le condizioni in cui l'individuo vive |
Dimostrazione di tutte le casistiche per induzione su 
Dato che a questo punto la dimostrazione è un fatto meccanico, mostrerò solo la prima (le altre saranno analoghe). Supponiamo che valga:
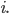
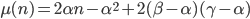
in particolare
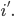
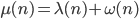
ovviamente con:
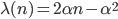
e
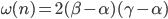
Verifichiamola per 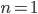 . Un quadrato ridotto alla sola cella con il numero 1 contiene esattamente 0 celle multiple di un qualsiasi intero dato dal prodotto di due primi differenti.
. Un quadrato ridotto alla sola cella con il numero 1 contiene esattamente 0 celle multiple di un qualsiasi intero dato dal prodotto di due primi differenti.
D'altro canto 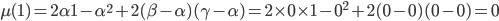
Dobbiamo quindi dimostrare che:
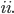
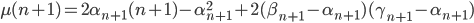
Ma, per definizione della casistica in cui ci troviamo, sappiamo che:
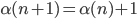 e, analogamente:
e, analogamente:
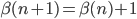 e
e
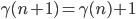
quindi otteniamo:
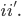
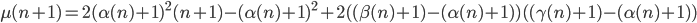
che, dopo semplici calcoli, porta a:
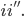
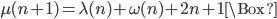 .
.
Le altre casistiche si risolvono con sostituzioni basate su analoghi ragionamenti.
